I Integrating discs to find the gravitational force of a sphere

[kairama15]

I am attempting to prove Newton's shell theorem. There are multiple solutions to this problem, but I am attempting a solution involving adding up the gravitational force of an infinite number of infinitely small disks that are placed together (the discs facing a point mass "m") to form a sphere. I am only focused on this approach as I am interested in this particular method of the proof.

known equations:
Force of gravity of a disc distance "d" away and of radius "a" = (2*G*M*m/a^2)*(1-d/sqrt(d^2+a^2)) (got from https://sciphy.in/gravitational-field-due-to-uniform-disc/ ; and I am comfortable with this equation and its derivation)

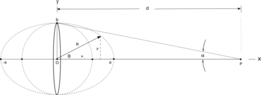
So, if I place a small point mass m at the origin of the xyz axis, and a disk whose center is distance x along the x-axis away from the origin, and the very thin disc is of weight "dM" the force of gravity of the disk is:

F=(2*G*m*dM/a^2)*(1-x/sqrt(x^2+a^2))

But suppose I have a sphere of radius "r" made of an infinite number of infinitely small discs at that same distance away, the height "a" of the surface of the sphere (or discs for that matter) above the x-axis is :
a=sqrt(r^2-(x-d)^2) (note that: if x=d, a=r. if x= (d-r) or (d+r), a=0) (This equation is simply the equation of a circle with radius R displaced from a distance "d" from the origin).

I also know the mass of the thin disc "dM" will change depending on its radius as the discs change shape as they stack together to make a sphere. And the weight of a small disc will be: dM=M*pi*(R^2-(x-d)^2)*dx / ( (4/3)*pi*R^3). I got this equation noticing that a thin slice of a sphere will have volume of : area*dx / volume of a sphere. The area is just pi*radius^2 where the radius follows the function sqrt(R^2-(x-d)^2). (note how this small mass of dM is intuitive when analyzed: If this dM is integrated from -R to R, dM=M, as we would expect for the full weight of the disc. And, at x= (d-r) or (d+r), dM=0 because the disc is infinitely small.)

Plugging dM and "a" into the above equation, I get:
F = [ (2*G*M*pi*(R^2-(x-d)^2) / ( (4/3)*pi*R^3 * (R^2-(x-d)^2) ] * (1-x/sqrt(x^2+R^2-(x-d)^2) ) .

Simplifying,
F= [ 3*G*M/(2*R^3) ] * ( 1 - x/sqrt(x^2+R^2-(x-d)^2 ) * dx

Integrating this from one end of the set of discs (d-r) to the other end of the set of discs (d+r), I get a really crazy integral and it doesn't simplify to GMm/d^2 as Newton so famously described. Any help on where I am going wrong setting up this integral?

 

[Hiero]

Ive deleted my post because after @Simon Bridge ’s reply I’ve realized I misunderstood your setup (when you said you were trying to prove the shell theorem I imagined you meant for a thin shell not for a solid sphere, whoops! It also confused me that you say “infinitely small disks”... but maybe you mean infinitely thin?)

 

[Simon Bridge]

A clear statement of the setup is important discipline. Start with a diagram showing everything you are interested. Describe the whole setup up front... don't just add bits as you go.

By my reading you are lining up the disks and the test mass so that they are all co-axial. ie. the centers of the disks are on the x axis, and so is the point mass... and the x-axis is perpendicular to the circular faces of the disks. The disks form a sphere radius r and mass M, of uniform density, centered on x=d; while a test mass m is at the origin.
Do I understand you correctly?

You are basically slicing the sphere into many thin disks and summing the effect of each disk separately?

For each disk you asserted, as already sufficiently proved, that:

"F=(2*G*m*dM/a^2)*(1-x/sqrt(x^2+a^2))" as the weight (force of gravity on) of the test mass due to the disk.
You use "mass" and "weight" interchangeably.
Stop that, it leads to sloppy thinking. The "force of gravity" is the weight. That is what you are calculating the formula for.

This is: $$dF = \frac{2Gm\; dM}{a^2}\left( 1 - \frac{x}{\sqrt{x^2+a^2}} \right)$$

You noticed that dM is a function of x... also "a", the "height" (you mean: "radius") of each disk is a function of x.

The mass of a disk between x and x+dx is given by:
$$dM(x) = \pi a^2(x)\frac{M}{V}\; dx \; dx \; : \; \frac{M}{V} = \frac{3M}{4\pi r^3}$$

The radius of each disk is given by:
$$a^2(x) = r^2-(x-d)^2$$

Put all that together and I get something like:
$$dF = \frac{3GMm}{r^3}\left[ 1-\frac{x}{\sqrt{x^2+r^2-(x-d)^2}} \right]\; dx$$

... which needs to be integrated over $x-d < x < x+d$.

Are you following this? (BTW: also check my algebra, I am known to get things wrong.)
Is there a difference with what you got?

Look for a transformation ... ie: shift the coordinates so the sphere is centered on the origin: shifts that "d" out of the messy part.

Basically, the process of turning that into something that is easier to do is the same as starting out with a nicer setup. Why do harder maths than you have to?

I am thinking that you are going about things about right, but your description shows a problem in keeping track of your working that gives you a high likelyhood of hard-to-spot errors in arithmetic and algebra. In above, if I have an algebra error, it should be easier for you to spot.

 

[kairama15]

Thanks for your responses. I agree that we should try to simplify the problem a bit more by changing how I we are setting it up. Instead of the sphere made of infinitely thin discs being placed a distance "d" away from the origin, let's put this series of objects centered at the origin and find the force from this sphere at a distance "d" away from the origin (at point (x,y)=(-d,0) ).

In this case, the equation for the force of any of these discs located a distance "L" away is:
F=(2*G*m*dM/a^2)*(1-L/sqrt(L^2+a^2)) where m is the mass at the point (-d,0), dM is the mass of one of the infinitely thin discs, a is the radius of the disc, and L is the distance between the disc and a point located at (x,y)=(-d,0).

The distance "L" from the point to any of the discs will be dependent on the location of the disc away from the origin. This distance "L" will be "d+x" where x will be ranging from -R to +R.

The radius "a" of any of the discs will be dependent on the location of the disc away from the origin. The discs will be stacked together to make a sphere whose crosssection will be a circle following the equation a=sqrt(R^2-x^2) where R is the radius of the sphere and x will range from -R to +R.

dM is the amount of mass in an infinitely thin disc. This thin disc's volume is pi*a^2*dx and the total amount of mass in a sphere of volume is (4/3)*pi*R^3. Using the above value for "a", dM=pi*(R^2-x^2)*dx/((4/3)*pi*R^3). Or simplified: dM=3*M*(R^2-x^2)*dx/(4*R^3). Note how dM integrated from -R to R equals M, the mass of the sphere.

Replacing L with "d+x" and replacing "a" with sqrt(R^2-x^2) and dM with 3*M*(R^2-x^2)*dx/(4*R^3) yields:
F= (2*G*m*(3*M*(R^2-x^2)/(4*R^3))/sqrt(R^2-x^2)^2) * ( 1-(d+x)/sqrt((d+x)+R^2-x^2) ) *dx
simplifying:
F= (3*G*m*M/(2*R^3)) * ( 1 - (d+x)/sqrt( (d+x)^2+R^2-x^2) ) ) * dx

Integrating this force with respect to x from -R to +R, and after quite a complicated integral and lots of cancelling, I'm left with Newton's shell theorem:
F=G*M*m/d^2

Thanks for your help! Simplifying the problem made it easier. You folks on this forum are always helpful.

What a beautiful proof - seeing everything become complicated and then simplify to such a remarkable equation. It's like art.

 

[MarkL]

I've never seen it done like this. Usually it involves integrating shells from 0 to R.
Start with the gravitational force from a disk centered at the origin, a distance d from the point P, as shown in the figure. The integration is standard and the force equals either equation:

\begin{align*}
& 2\pi Gm\sigma t(1 - \cos(\alpha)) \\
& 2\pi Gm\sigma t[1 -\frac{{d}}{\sqrt{R^2+d^2}}]
\end{align*}

where G is the gravitational constant, $m$ the mass at P, $\sigma$ the volume density of the disk, R the disk radius, $d$ the distance of P from the disk and $t$ ($= dx$) the disk thickness.

With the radius of the disk and the distance to P now a function of x, we make the following substitutions in the second equation and just integrate to get,
\begin{align*}
& 2\pi Gm\sigma[1 -\frac{{d-x}}{\sqrt{(R^2-x^2)+(d-x)^2}}]dx \\
& 2\pi Gm\sigma[\int_{-R}^{R}dx -\int_{-R}^{R}\frac{{(d-x)dx}}{\sqrt{(R^2-x^2)+(d-x)^2}}] \\
& 2\pi Gm\sigma[2R - (2d/a) \sqrt{ax+b}|_{-R}^{R} + (2/3a^2) (ax-2b)\sqrt{ax+b}|_{-R}^{R}] \\
& 2\pi Gm\sigma[2R - 2R + 2R^3/3d^2] = GMm/d^2
\end{align*}
Where $a=-2d$ , $b=R^2+d^2$ and $M=4\pi \sigma R^3/3$

Substituting R for d, the force on the surface of the sphere at R can be factored as follows and much easier to integrate:
\begin{align*}
& 2\pi Gm\sigma[\int_{-R}^{R}dx -\int_{-R}^{R}\frac{{(R-x)dx}}{\sqrt{(R^2-x^2)+(R-x)^2}}] \\
& 2\pi Gm\sigma [\int_{-R}^{R}dx - \int_{-R}^{R}\frac{{\sqrt{(R-x)}dx}}{\sqrt{2R}}] = GMm/R^2
\end{align*}

 

[MarkL]

With the radius of the disk and the distance to P now a function of x, we make the following substitutions in the second equation and just integrate to get,
\begin{align*}
& 2\pi Gm\sigma[1 -\frac{{d-x}}{\sqrt{(R^2-x^2)+(d-x)^2}}]dx \\
& 2\pi Gm\sigma[\int_{-R}^{R}dx -\int_{-R}^{R}\frac{{(d-x)dx}}{\sqrt{(R^2-x^2)+(d-x)^2}}] \\
& 2\pi Gm\sigma[2R - (2d/a) \sqrt{ax+b}|_{-R}^{R} + (2/3a^2) (ax-2b)\sqrt{ax+b}|_{-R}^{R}] \\
& 2\pi Gm\sigma[2R - 2R + 2R^3/3d^2] = GMm/d^2
\end{align*}
Where $a=-2d$ , $b=R^2+d^2$ and $M=4\pi \sigma R^3/3$

Substituting R for d, the force on the surface of the sphere at R can be factored as follows and much easier to integrate:
\begin{align*}
& 2\pi Gm\sigma[\int_{-R}^{R}dx -\int_{-R}^{R}\frac{{(R-x)dx}}{\sqrt{(R^2-x^2)+(R-x)^2}}] \\
& 2\pi Gm\sigma [\int_{-R}^{R}dx - \int_{-R}^{R}\frac{{\sqrt{(R-x)}dx}}{\sqrt{2R}}] = GMm/R^2
\end{align*}

If anyone is interested...
The equation for the ellipse is $x^2/a^2 + y^2/b^2 = 1$, $a > b$. Substituting $a$ for $d$ above and solving for $y$, the equations become
\begin{align*}
& 2\pi Gm\sigma \int_{-a}^{a}[1 - \frac{(a-x)}{\sqrt{(b^2-(b^2/a^2)x^2)+(a-x)^2}}]dx \\
\text{or} \\
& 2\pi Gm\sigma \int_{-a}^{a}[1 - \frac{(a-x)}{\sqrt{Ax^2+Bx+C}}]dx
\end{align*}
with
$$A = 1 - b^2/a^2, B = -2a, C = a^2 + b^2$$
The gravitational attraction on the surface of the ellipsoid at point $a$ - which is all you need - becomes
\begin{align*}
& 2\pi Gm\sigma [x - (a + B/A)E + D/A]|_{-a}^{+a}
\end{align*}
where
$$D = \sqrt{Ax^2 + Bx + C}~~~~~ \text{ and } ~~~~~E = ln(2 \sqrt{A}D + 2Ax +B)/\sqrt{A}$$
which can be programmed.