Integration Bounds for E-field Calcualtion

[Ren Figueroa]

Hi guys.
I’m looking at the brute force way at getting the E-field for a uniformly spherical charge distribution. The location of the E-field of interest is anywhere outside of the sphere. Here are some images

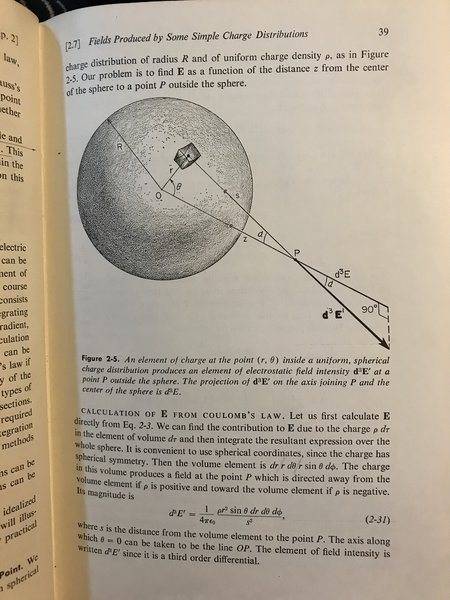
Everything makes sense. I’m just not sure why the bounds for ‘s’ where z-r to z+r. From my perspective, z+r is the left hemisphere while z-r is the right hemisphere because we can consider the relationship between s, r, and z from the vector relation s=z-r. If i set the positive axis to point to the left, if sort of makes sense to integrate from z+r to z-r but this would obviously yield a negative result. So, I’m curious about detmining the proper bounds.

 

[kuruman]

I think what happens here is that when the book does the change of coordinates, it matches limits of integration appropriately. When θ = 0 (lower limit), s = z - r and when θ = π (upper limit), s = z + r.

By the way, is this Stratton's book you're looking at?

 

[Ren Figueroa]

I'm so embarrassed. You're right. Just plugging in the prior bounds gets the result. I thought of doing that but I sort of just eye-balled it and thought it wouldn't give me the result I was looking for. Sorry about that.

It's a text by Corson and Lorrain. Definitely not as rigorous as the Stratton text.