Integration by filaments or integration by strate?

[Amaelle]

Homework Statement

look at the image

Relevant Equations

cylindrical coordinates
integration by strates
integration by filaments

Greetings
While solving the following exercice, ( the method used is the integration by filaments and I have no problem doing it this way)

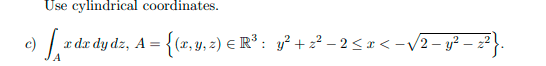
here is the solution

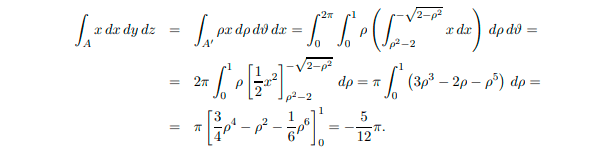
My question is the following:
I want to do the integration by strate and here is my proposition

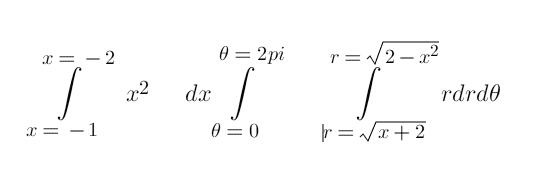
is that even correct?
I would like to know if there is cases when switching between the two methods of integration is not possible?
thank you in advance!

 

[vela]

I've never heard of "integration by strate." Could you explain what this means?

 

[Amaelle]

Certainly look at the image

it means doing the integration by rings and then integrating by hight

 

[vela]

Oh, okay. In the US, I think that technique is referred to as the disc method.

 

[vela]

You should be able to use that method, but you're going to have to break the integral up into two integrals, one from $x=-2$ to $x=-\sqrt{2}$ and one from $x=-\sqrt{2}$ to $x=-1$.

 

[Amaelle]

thank you very much , indeed I used your insights to solve the question under the disk method

but the only way I could find out was to

and then substructing the sphere from the paraboloid
I would be very grateful if you could elaborate more about the setting of your method and why you need to split the integration this way?
thank you!

 

[vela]

To keep it simple, I'm going to consider volume integrals but the same ideas apply to your problem.

When you do the integrals over $r$ and $\theta$, you end up with an integral of the form
$$\int_{x_1}^{x_2} \pi r^2 \,dx$$ where we can identify $\pi r^2$ as the area of the disk and $dV = \pi r^2\,dx$ as the volume of the infinitesimal slice. In this particular problem, from $x=-2$ to $x=-\sqrt{2}$, the volume is given by an integral of that form. However, from $x=-\sqrt{2}$ to $x=-1$, you have a disk with a hole in the middle with area $\pi(r_{\rm outer}^2-r_{\rm inner}^2)$. Hence, the volume of that portion is given by
$$\int_{x_1}^{x_2} \pi (r_{\rm outer}^2-r_{\rm inner}^2) \,dx.$$ Because you have two different integrands, you need to do the integrals for each range separately.

Note that you can manipulate your integrals similarly:
\begin{align*}
I &= \int_{-2}^{-1} \int_0^{2\pi} \int_0^{\sqrt{2-x^2}} xr\,dr\,d\theta\,dx
-\int_{-\sqrt 2}^{-1} \int_0^{2\pi} \int_0^{\sqrt{x+2}} xr\,dr\,d\theta\,dx \\
&= \int_{-2}^{-\sqrt{2}} \int_0^{2\pi} \int_0^{\sqrt{2-x^2}} xr\,dr\,d\theta\,dx
+\int_{-\sqrt{2}}^{-1} \int_0^{2\pi} \int_0^{\sqrt{2-x^2}} xr\,dr\,d\theta\,dx
-\int_{-\sqrt 2}^{-1} \int_0^{2\pi} \int_0^{\sqrt{x+2}} xr\,dr\,d\theta\,dx \\
&= \int_{-2}^{-\sqrt{2}} \int_0^{2\pi} \int_0^{\sqrt{2-x^2}} xr\,dr\,d\theta\,dx
+\int_{-\sqrt{2}}^{-1} \int_0^{2\pi} \int_{\sqrt{x+2}}^{\sqrt{2-x^2}} xr\,dr\,d\theta\,dx
\end{align*} The limits on the $r$ integral are different for $x=-2$ to $x=-\sqrt{2}$ and for $x=-\sqrt{2}$ to $x=-1$.

 

[Amaelle]

thanks a million!