SUMMARY
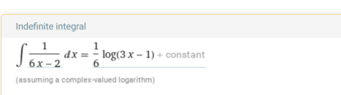
The integration of the function $$\int \dfrac{1}{6x-2} dx$$ can be approached using two methods: Wolfram's method, which assumes a complex-valued logarithm, and Symbolab's method, which adheres to the standard definition of the natural logarithm for positive real numbers. Both methods yield correct results, with Wolfram's approach applicable to complex analysis and Symbolab's suitable for real analysis. The key takeaway is that both answers are equivalent under the condition that $$6x-2 > 0$$, or $$x > \frac{1}{3}$$, while they diverge for $$x < \frac{1}{3}$$.
PREREQUISITES
- Understanding of integral calculus, specifically the integration of rational functions.
- Familiarity with the natural logarithm function and its properties.
- Knowledge of complex analysis, particularly the concept of analytic continuation.
- Ability to manipulate algebraic expressions and perform substitutions in integrals.
NEXT STEPS
- Study the properties of the natural logarithm and its domain restrictions.
- Learn about analytic continuation and its implications in complex analysis.
- Explore the differences between real and complex integration techniques.
- Practice integrating rational functions using various methods, including substitution.
USEFUL FOR
Students and professionals in mathematics, particularly those focusing on calculus, complex analysis, and integration techniques. This discussion is beneficial for anyone seeking to understand the nuances between different approaches to integration.