Integration using the reduction formula

[studentxlol]

Read the math in the image below

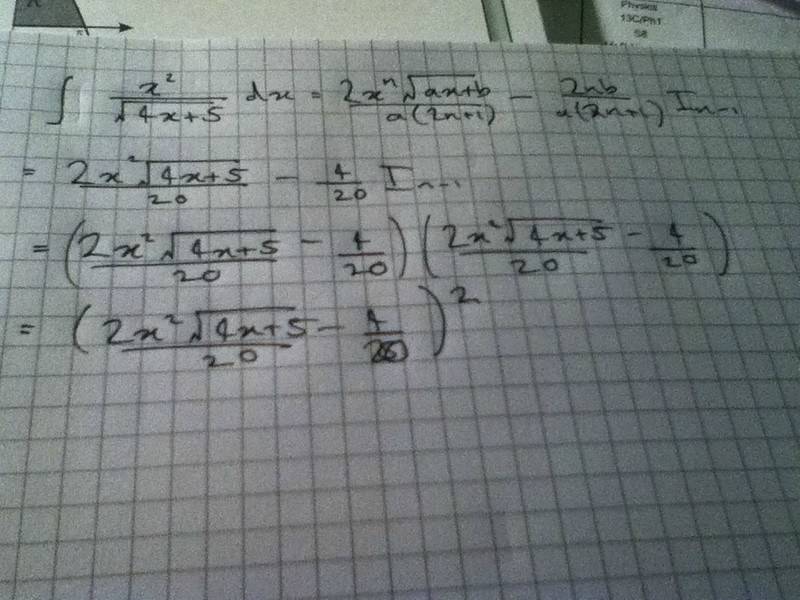
Is it possible to integrate the rational function using that reduction formula. If yes, how do I go about doing it?

Keep it simple, I'm new to this (And I missed a lesson)

Thanks!

 

[vela]

You have
$$I_n = \int \frac{x^n}{\sqrt{ax+b}}\,dx$$ so you're starting with n=2. When you apply the formula and simplify, you should get
$$I_2 = \frac{x^2\sqrt{4x+5}}{10} - I_1$$ You made a mistake in the coefficient of I₁, so recheck your work getting the second line. Now apply the same formula to expand I₁. You'll end up with an expression with I₀ which you should know how to integrate.