mm2424
- 43
- 0
Homework Statement
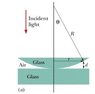
A lens with radius of curvature R sits on a flat glass plate and is illuminated from above by light with wavelength λ (see picture below). Circular interference patterns, Newton's Rings, are seen when viewed from above. They are associated with variable thickness d of the air film between the lens and the plate. Find the radii r of the interference maxima assuming r/R <<1.
Homework Equations
2L = (m + 1/2) λ
The Attempt at a Solution
I understand that we will use 2L = (m + 1/2) λ here. However, I can't figure out how we relate d to R or r. I have my professor's answer key, and he defines θ as the top angle in the picture (formed by R and the normal line to the glass surfaces). He then says that r/R = sinθ which equals θ. Then, he says d = R(1-cosθ) and uses the expansion of cosθ = 1 - θ^2/2 + θ^4/4!, etc.
I can't wrap my head around how he found d = R(1-cosθ). If someone can help me see it, I would be greatly appreciative.
Thanks!