Interpretation of 'homologous to' - Munkres analysis of homology grou

[Math Amateur]

I am reading James Munkres' book, Elements of Algebraic Topology.

Theorem 6.2 on page 35 concerns the homology groups of the 2-dimensional torus.

I would appreciate some help with interpreting the term 'homologous to' as it relates to a part of the proof of Munkres' Theorem 6-2 concerning the homology groups of the torus.

The relevant part of the proof is as follows: (see end of my post for a complete copy of Theorem 6.2)

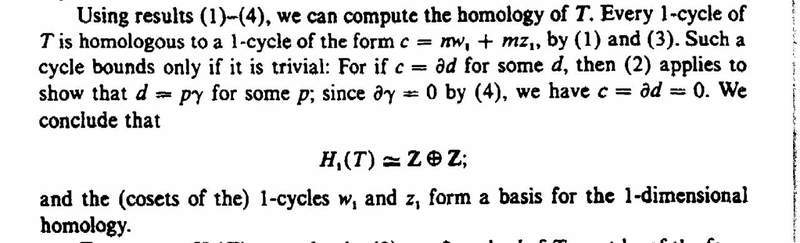
It seems that in proving that H_1 (T) = \mathbb{Z} \oplus \mathbb{Z} Munkres has shown that every 1-cycle of T is homologous to a 1-cycle c of the form c = n w_1 + m z_1, and, further, that the only boundaries of such cycles are trivial i.e. there are no boundaries of these cycles.

I basically follow the details of Munkres analysis ...

BUT ... to show that H_1 (T) = \mathbb{Z} \oplus \mathbb{Z} we should show that every on cycle is of the form c = n w_1 + m z_1, and, ... ... etc ...

... and not just that every 1-cycle is homologous to such as cycle ie that for every cycle c_1 we have:

c - c_1 = \partial d for some d ... ...

or is this just the same ...

Can someone please clarify this issue for me.

The details of Theorem 6.2 and its proof are as follows:

The definition of homologous is given in the following text from Munkres:

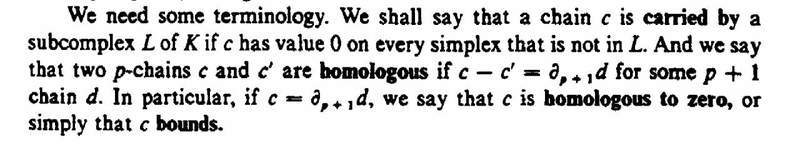
Hope someone can help,

Peter

 

[homeomorphic]

Very messy post. No wonder no one responded. Anyway, no, you don't need to prove that every cycle is of that form because that would be false. There are tons of cycles that are not of that form. The boundary of every single triangle in the diagram would be a cycle that is not of that form. You are modding out by boundaries of 2-cells, therefore they don't matter. Basically, you are adding a bunch of stuff that has been set equal to zero in order to push it to the edge. Pushing stuff into the boundary doesn't affect anything in homology because you mod out by that stuff.

 

[Math Amateur]

Thanks homeomorphic, your post was most helpful to me ...

My statement, implying that in order ".. to show that H_1 (T) = \mathbb{Z} \oplus \mathbb{Z} we should show that every on cycle is of the form c = n w_1 + m z_1 " was quite wrong as you point out ... there are indeed many cycles in L that are not of this form!

Now, yes ... I think I follow your general clarification of what is going on in Munkres' Theorem 6.2, but I would really like to follow the specific logic of Munkres' argument that he presents in the proof of Theorem 6,2 as follows: (see statement and proof of Theorem 6.2 in the post above)

----------------------------------------------------------------------------------------------

Using results (1)-(4), we can compute the homology of T. Every 1-cycle of T is homologous to a 1-cycle of the form c = n w_1 + m z_1, by (1) and (3). Such a cycle bounds only if it is trivial: for if c = \partial d for some d, then (2) applies to show that d = p \gamma for some p; since \partial \gamma = 0. We conclude that:

H_1 (T) = \mathbb{Z} \oplus \mathbb{Z}

and the (cosets of the) 1-cycles w_1 \text{ and } z_1 form a basis for the 1-dimensional homology.

----------------------------------------------------------------------------------------------

Munkres first statement is that any 1-cycle of T, say c', is homologous to a 1-cycle of the form c = n w_1 + m z_1 ... that is:

c' - c = \partial_2 d' for some 2-chain d' ... ... ... ... (5)

Munkres then states that such a cycle as c bounds only if it is trivial - that is:

... if c = \partial d then c = 0 ... ... ... ... (6)

BUT then Munkres writes:

"We conclude that:

H_1 (T) = \mathbb{Z} \oplus \mathbb{Z}"


What is the rigorous logic for this conclusion ... why precisely does this conclusion follow from (5) and (6) above?


Can someone please help me with this?

Would appreciate help,

Peter

EDIT: It would help me enormously, for example, if someone could show me what Z_1 (T) and B_1 (T) were - indicating how these groups were derived from Munkres' analysis above!

 

[homeomorphic]

He's just saying you don't need to mod out by anything further once you push everything to the edge. If you have a 2-chain, the only way its boundary could be of the form n w_1 + m z_1 is if it is a multiple of all the 2-simplices added together (I'm being sloppy about orientation here). Argue by contradiction. If any of those 2-simplices is missing from the sum, you'll get terms that are not on the edge of the square when you apply the boundary operator (i.e. it wouldn't be of the form nw_1 + m z_1).

Z_1(T) is all the guys that "close up" and formal sums of such things. B_1(T) is all the boundaries of the triangles and sums of those. It isn't just matter of knowing what those are and then modding out, though. That could get pretty ugly, so it is better to do what Munkres is doing and be more clever and indirect about it.

 

[WWGD]

You may be overlooking some details. To say what homeomorphic said in other words, Munkres is just using the algebraic definition of homology as the quotient $$ Ker d_n/Im (d_{n+1})$$ (where the $d_i$ 's are the boundary operators) , a.k.a, cycles/boundaries, the algebraic (as modules here) quotient Z(T)/B(T). Since every cycle is of the form nw_1+ mz_1 for m,n integers, we get that $Z_1(T)$, the 1-cycles of T are isomorphic ( maybe they're related to homeomorphic ;) ) to $\mathbb Z (+) \mathbb Z$ . Similarly, Munkres concluded that the (module of) bounding cycles is the trivial module B_1(T)= {0} . We then get, using the algebraic quotient definition, we get the quotient of modules: $$H_1(T)=Z_1(T)/B_1(T) =Z_1(T)$$ (notice the strange thing that , in a sense, you can divide by zero ).

 

[homeomorphic]

That doesn't sound quite right. Z_1(T) isn't Z plus Z in this case. Only AFTER modding out by the boundaries can we represent all cycles by guys carried by the boundary square, so we're already in homology (sort of). You're really modding out in stages, it seems. Mod out by enough to push everything to the boundary and see whether you've modded out by enough stuff. The conclusion is, yes, you modded out by enough stuff and you've arrived at the homology.

One weird thing about homology is that it ends up being a topological invariant, even though it's defined in a non-invariant way. Specifically, the simplicial chain complex depends on your triangulation. It's got a copy of Z for each symplex in each dimension. And similarly, the group of cycles (and boundaries) is still not topologically invariant. It, too, depends on the triangulation. When you haven't yet modded out by the boundaries, it's as if the 2-skeleton is entirely absent. So, it looks to me like you get a copy of Z for each triangle in the 1-skeleton, if you really wanted to know what Z_1 is in this case. But you don't actually need to know what Z_1 is.

And as I said, B_1 is all formal sums of 2-simplices in the triangulation.

 

[WWGD]

Yes, I was taking some results for granted, and just dotting some t's, crossing some I, e.g., I accepted the fact that all cycles (are homologous to cycles) of the form $m_1z_1+m_2z_2$; I did not go thru the argument in detail. And actually , if by topological invariant you mean preserved under homeomorphism, homology is even preserved under homotopy equivalence.

 

[homeomorphic]

My point is that that Z plus Z isn't really Z_1 with respect to the triangulation. Z_1 with respect to the triangulation would be the whole big thing generated by all the boundaries of the triangles. So, it's okay, as long as you don't call it Z_1. It's some quotient of Z_1, which turns out to be the homology.

 

[homeomorphic]

And technically, B_1 is not 0. It's just that the subgroup of B_1 generated by the boundary square is trivial.

 

[WWGD]

Yes; I took the post from the point where Amateur wanted to know how Munkres had arrived to the homology _after_ the issues you mention had been addressed, which is what I understood Amateur wanted ; I did not address those issues myself.

 

[Math Amateur]

Thanks WWGD and homeomorphic ... you have helped me to get a much better general picture of the homology groups involved ... but I am still trying to build a precise understanding of Munkres argument ...

Let me state where I am with Munkres' arguments now ... and then pose a question ...We have that every 1-cycle c' of T is homologous to a 1-cycle of the form c = n w_1 + m z_1 by (1) and (3) - so more precisely we have

c' - c = \partial_2 d for some boundary d

\Longrightarrow every 1-cycle c' = c + \partial_2 d

\Longrightarrow c' = n w_1 + m z_1 + \partial_2 d

(ie every 1-cycle is of the form c' = n w_1 + m z_1 + \text{ (some boundary) }

So now I should be able to give a precise argument from here ...

But I only have a general picture ,,,

One question I do have is how do you get from every cycle c' being of the form c' = n w_1 + m z_1 + \partial_2 d to H_1 (T) = Z_1 (T) / B_1 (T) = \mathbb{Z} \oplus \mathbb{Z} ...

I can see how if every cycle c' was of the form c' = n w_1 + m z_1 that Z_1(T) would be equal to \mathbb{Z} \oplus \mathbb{Z} since n and m each run through all the integers ... but of course the relation c' = n w_1 + m z_1 is not true ... we actually have c' = n w_1 + m z_1 + \partial_2 d ... so any help on this specific point would be welcome!It would also help me a great deal if I could actually describe the cosets of H_1 (T) = Z_1 (T) / B_1 (T) ... but I am not really clear about the process going on ... or the nature of the cosets involved ...

Thinking aloud ...

If we have cycles c_1, c_2 \in Z_1 (T) such that

c_1 = 2 w_1 + 2 z_1 + \partial_2 d_1

and

c_2 = w_1 + z_1 + \partial_2 d_1

then

c_1 - c_2 = w_1 + z_1 ...

... ? ... are these two cycles in the same coset ... ?

I think I am confused at this stage ...

Can you help me to describe the relevant cosets in a precise way?

Peter

 

[WWGD]

Sorry, homeomorphic, I do welcome the geometric perspective, but I thought Amateur wanted to (at least) temporarily by pass that. Please feel free to add to the geometric perspective, though; I do know we can work with the formal chain groups and formal chains , formally compute boundaries, and use the fundamental domain to narrow-down the set of homology cycles; I thought amateur wanted to take that for granted for a little while, but the geometric perspective is also nice to have.

 

[homeomorphic]

but of course the relation c′=nw1+mz1 is not true ... we actually have c′=nw1+mz1+∂2d ... so any help on this specific point would be welcome!

Actually, it IS true. But it's true in homology, not in Z_1. It's true when you mod out by boundaries. It's the same thing as if I said 1 = 1+3 mod 3.

It would also help me a great deal if I could actually describe the cosets of H1(T)=Z1(T)/B1(T) ... but I am not really clear about the process going on ... or the nature of the cosets involved ...

Cosets of B_1 in Z_1 are of the form 1-cycle + 1-boundary, where the 1-cycle is fixed and the boundaries vary over all possible boundaries. So, basically, you take your representative cycle and you add every possible boundary to it. Just as a coset in Z mod 3 would be something like...1-6, 1-3, 1, 1 + 3, 1+ 6, 1+9...

Here, 1 is playing the role of your chosen, fixed cycle and the multiples of 3 are playing the role of the boundaries.

If we have cycles c1,c2∈Z1(T) such that

c1=2w1+2z1+∂2d1

and

c2=w1+z1+∂2d1

then

c1−c2=w1+z1 ...

... ? ... are these two cycles in the same coset ... ?

I think if you think of the Z mod n analogy, the answer should be clear. Subtract 2 cosets...

Edit: Did you mean to ask if c2, and c1-c2 are in the same coset? Then, yes, since they are both w1+z1 mod boundaries.