Interpreting a thermodynamics formula using a picture

[PhysicsKush]

Homework Statement

$$ \frac{\partial \Gamma}{\partial p} \Bigg|_{t} = \frac{\partial \Gamma}{\partial p} \Bigg|_{v} + \frac{\partial v}{\partial p}\Bigg|_{t} \frac{\partial \Gamma}{\partial v} \Bigg|_{p}$$

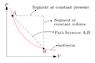
Interpret this formula by using words or a picture (ie. the change in Gamma when we pressurize a gas along an isotherm, is equal to...).

Relevant Equations

$$ \Gamma(p,v) = vp^2$$
$$ pv=t$$

I notice that $pv=t$ looks like the ideal gas law but with $T$ in units of energy. I know that $pV = \text{constant}$ means that the pressure of a gas decreases as you expand it (Boyle-Mariotte's law), explaining for instance how we breathe.

I guess I could put everything in words even though it will be a paragraph long and probably incorrect :

"The change in Gamma when we pressurize a gas along an isotherm is equal to the change in Gamma when we pressurize that gas along an isovolumetric process , with additionally the product between the change in volume during pressurization along an isotherm and the change in Gamma under a dynamic contrast along an isobar",

but I'm curious to see how this could be represented with a picture.

 

[Chestermiller]

Here's a hint. Start out by drawing a short section of an isotherm on a PV diagram.

 

[PhysicsKush]

Here's a hint. Start out by drawing a short section of an isotherm on a PV diagram.

Thank you for your insightful hint. I came to the conclusion, that the formula as defined represents an isothermal compression process of an ideal gas.

 

[Chestermiller]

Thank you for your insightful hint. I came to the conclusion, that the formula as defined represents an isothermal compression process of an ideal gas.

Let's see your diagram, showing how the equation plays out.

 

[PhysicsKush]

Let's see your diagram, showing how the equation plays out.

After reconsidering,I think it is actually an isothermal expansion since the slope $\frac{\partial v}{\partial p}\big|_{t}$ is multiplied by $\frac{\partial \Gamma}{\partial v}\big|_{p}$ ,which is along the $x$ direction.

 

[Chestermiller]

After reconsidering,I think it is actually an isothermal expansion since the slope $\frac{\partial v}{\partial p}\big|_{t}$ is multiplied by $\frac{\partial \Gamma}{\partial v}\big|_{p}$ ,which is along the $x$ direction.

What they are looking for is two alternate paths connecting two adjacent point on the isotherm. One path is directly between the two points. The other has one segment at constant pressure and a second segment at constant volume. The diagram should show that the two alternate paths deliver the same change in gamma.

 

[PhysicsKush]

What they are looking for is two alternate paths connecting two adjacent point on the isotherm. One path is directly between the two points. The other has one segment at constant pressure and a second segment at constant volume. The diagram should show that the two alternate paths deliver the same change in gamma.

I think I successfully illustrated what you described to me. If that is indeed correct, I'm very curious to know how how you were able to interpret the given PDE formula and come up with this conclusion, because I'm not able to do that. Thank you again sir.

 

[Chestermiller]

I think I successfully illustrated what you described to me. If that is indeed correct, I'm very curious to know how how you were able to interpret the given PDE formula and come up with this conclusion, because I'm not able to do that. Thank you again sir.

I don't know. Just experience, I guess.

 

[PhysicsKush]

I don't know. Just experience, I guess.

Well, I can not submit this picture since I don't understand how we arrived at this conclusion. I shall keep on searching for an alternate answer. Thank you again for your help !

 

[Chestermiller]

OK. I'm going to take another shot at this. On a PV diagram, show some lines of constant T, and some crossing lines of constant $\Gamma=vp^2$. Then show the line for a change in $\Gamma$ along a line of constant T. I think that this will make more sense to you.

 

[Chestermiller]

If we increase pressure by $\delta P$ at constant temperature, the function $\Gamma$ increases from $\Gamma_1$ to $\Gamma_2$. But. if we increase pressure by $\delta P$ at constant volume, the function $\Gamma$ increases by more, from $\Gamma_1$ to $\Gamma_3$. So, in the latter case, if we want to get the change and constant temperature, we need to add an additional term equal to $\left(\frac{\partial V}{\partial P}\right)_T\left(\frac{\partial \Gamma}{\partial V}\right)_P\delta P=-(\Gamma_3-\Gamma_2)$

 

[PhysicsKush]

View attachment 269284
If we increase pressure by $\delta P$ at constant temperature, the function $\Gamma$ increases from $\Gamma_1$ to $\Gamma_2$. But. if we increase pressure by $\delta P$ at constant volume, the function $\Gamma$ increases by more, from $\Gamma_1$ to $\Gamma_3$. So, in the latter case, if we want to get the change and constant temperature, we need to add an additional term equal to $\left(\frac{\partial V}{\partial P}\right)_T\left(\frac{\partial \Gamma}{\partial V}\right)_P\delta P=-(\Gamma_3-\Gamma_2)$

WOW ! I think I understand now ,all the pieces are connecting together !

Thank you so much for having persisted with me throughtout this. Couldn't thank you enough sir.