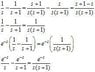shaqywacky
- 4
- 0
Hello again.
First off, I wasn't sure how to say this in the title but I'm not taking the inverse Laplace transform of a unit step function. I'm taking the Laplace transform of something that comes out to the unit step function.
I have this question, which is a similar version of the question I am trying to solve. This is also the solution but I have no idea what happened.
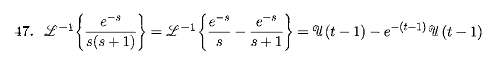
(sorry, I don't know why that is so small, click to make it bigger)
So the first part of that image is just the inverse Laplace transform I am trying to solve. The first step I saw was to do partial fractions. When I do that I get:
\frac{e}{s+1} + \frac{1}{s}
I'm omitting the inverse Laplace transform here because I don't know how to do it in latex.
But as you can see, the solution maunual got:
\frac{e^{-s}}{s} - \frac{e^{-s}}{s+1}
Clearly there is something I do not understand about this. I can get the correct answer after this, I just don't understand this step.
Any help would be greatly appreciated.
Thank you.
First off, I wasn't sure how to say this in the title but I'm not taking the inverse Laplace transform of a unit step function. I'm taking the Laplace transform of something that comes out to the unit step function.
I have this question, which is a similar version of the question I am trying to solve. This is also the solution but I have no idea what happened.
(sorry, I don't know why that is so small, click to make it bigger)
So the first part of that image is just the inverse Laplace transform I am trying to solve. The first step I saw was to do partial fractions. When I do that I get:
\frac{e}{s+1} + \frac{1}{s}
I'm omitting the inverse Laplace transform here because I don't know how to do it in latex.
But as you can see, the solution maunual got:
\frac{e^{-s}}{s} - \frac{e^{-s}}{s+1}
Clearly there is something I do not understand about this. I can get the correct answer after this, I just don't understand this step.
Any help would be greatly appreciated.
Thank you.
Last edited: