rustynail
- 53
- 0
I am starting to learn propositional calculus and am trying to make sense of the notation. I am trying to express the idea that sets A and B are equivalent. I want to know if the following statement is true and if it shows three equally valid ways of saying that A and B are the same set.
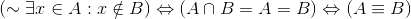
Thank you for your time. Any help and/or recommendations would be greatly appreciated.
Edit : Looking back at it, I think the first part does not imply that there are no elements of B that are not also in A. It does not eliminate the possibility that A is a subset of B. Should I write :
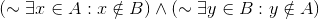
?
Thank you for your time. Any help and/or recommendations would be greatly appreciated.
Edit : Looking back at it, I think the first part does not imply that there are no elements of B that are not also in A. It does not eliminate the possibility that A is a subset of B. Should I write :
?
Last edited: