A Is energy really conserved?

[Ben tesoriero]

TL;DR

Do gyroscopic forces allow energy to be destroyed.

I built a device designed to brake angular velocity which seems to work based on below, i used a flexible shaft that could bow up and down so i could visually see what was happening for the prototypes.

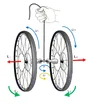
If you spin two wheels in opposite directions each with a magnitude of angular momentum L on a rigid shaft (equal magnitude opposite directions), then rotate the shaft at 90 degrees to the momentum vectors at constant angular velocity omega, then the resulting torques oppose each other causing a defection but no steady state angular velocity in the direction of the resulting torques..

You have energy in, 2 x L x omega^2, but you have no energy out as the resulting torques at steady state have no velocity.. (use the equation/ videos demonstrating gyroscopic precession to understand this). Ignoring any incidental friction losses, The magnitude of angular momentum of the wheels stays constant.

If you wish to test this more simply than i did, bolt two angle grinders back to back using a reasonable length of threaded bar with the heaviest discs you can find. When you try and turn them when running you will feel the resistance to rotation and hopefully see the deflection in the handles, using a less rigid shaft may assist in seeing this, or use two gyroscopic precession demonstration wheels, joined by a spring, hung centrally.

Does this not meet the definition of energy being destroyed?

 

[PeroK]

The experiment you propose is not clear from your description. It's not clear to me why you think energy is lost from a system of two spinning discs.

 

[wrobel]

Gyroscopic forces do not do work. Just by definition because the gyroscopic forces are $Q_j=\omega_{ij}(t,x)\dot x^i,$ where $\omega_{ij}=-\omega_{ji}$ and $x=(x^1,\ldots,x^m)$ are the generalized coordinates

 

[A.T.]

If you spin two wheels in opposite directions each with a magnitude of angular momentum L on a rigid shaft (equal magnitude opposite directions) ...

When you try and turn them when running you will feel the resistance to rotation

Why should there be resistance to rotation, if the total angular momentum of both wheels together is zero?