Ara wolf
- 1
- 0
- TL;DR
- I'm wondering why do we have a sinusoidal wave instead of a triangular wave when we describe a simple oscillation.
Hello everyone,
I'm a new member, and you might see me around from now on. I'm now on a path to understanding the mathematics behind a complicated mechanical machine. My knowledge is basically what I learned during my school days and also during university courses, and for me, it was mostly based on memorizing the formulas and doing homework! Now I'm trying to understand the real fundamentals. Before I start, I should apologize for my poor English, Please just bear with me. So here is my question:
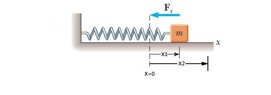
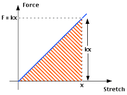
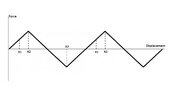
Imagine you have a system made of a spring and a mass on a frictionless surface, just like in the first picture. If you pull the mass away from its equilibrium position and reach X1, the restoration force of the spring at X1 will be F1. If you keep pulling it and reach the X2 point, you will have an F2. If X2=2.X1 then F2 should also be two times bigger than F1 based on the hook's low. correct? So the graph will be something like the second picture. Now imagine that after pulling it to X2 you let the object go, the spring will pull it, it goes all the way to the left, reaches -X2, and reaches -X2, and then comes back to X2. Since we have no friction, there will be no waste of energy, and the restoration force for any X should be the same any time it passes that point. it means if I want to stop the object with my hand at X1, I should do so by a applying a force as big as the one I applied the first time that I pulled the spring so far to X1 which is also as big as the restoration force of F1 but in the opposite direction. So it should exactly track the same graph of the second picture each time. That means the graph should be a triangular wave, like in the 3rd picture. And since the force is F=ma and your mass in this example is constant, the graph for acceleration should also look similar, but this movement is a simple harmonic oscillation, and the graph for acceleration in a simple harmonic system is shown as a sinusoidal wave! So am I losing some points? Is Hook's law not working, or is there a problem with my logic?
I'm a new member, and you might see me around from now on. I'm now on a path to understanding the mathematics behind a complicated mechanical machine. My knowledge is basically what I learned during my school days and also during university courses, and for me, it was mostly based on memorizing the formulas and doing homework! Now I'm trying to understand the real fundamentals. Before I start, I should apologize for my poor English, Please just bear with me. So here is my question:
Imagine you have a system made of a spring and a mass on a frictionless surface, just like in the first picture. If you pull the mass away from its equilibrium position and reach X1, the restoration force of the spring at X1 will be F1. If you keep pulling it and reach the X2 point, you will have an F2. If X2=2.X1 then F2 should also be two times bigger than F1 based on the hook's low. correct? So the graph will be something like the second picture. Now imagine that after pulling it to X2 you let the object go, the spring will pull it, it goes all the way to the left, reaches -X2, and reaches -X2, and then comes back to X2. Since we have no friction, there will be no waste of energy, and the restoration force for any X should be the same any time it passes that point. it means if I want to stop the object with my hand at X1, I should do so by a applying a force as big as the one I applied the first time that I pulled the spring so far to X1 which is also as big as the restoration force of F1 but in the opposite direction. So it should exactly track the same graph of the second picture each time. That means the graph should be a triangular wave, like in the 3rd picture. And since the force is F=ma and your mass in this example is constant, the graph for acceleration should also look similar, but this movement is a simple harmonic oscillation, and the graph for acceleration in a simple harmonic system is shown as a sinusoidal wave! So am I losing some points? Is Hook's law not working, or is there a problem with my logic?


