Jag1972
- 40
- 0
Hello Folks,
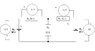
I have attached a DC circuit consisting of two opposing batteries and 3 resistors. The first step I took was to speculate on the direction of currents in both loops. I assumed the direction of conventional current for both loops, knowing full well that the maths will tell me if its correct by the operator in front of value. My results show that the middle branch has no volt drop across it as both currents are 180 degrees out of phase. The total voltage in the circuit is the sum of the two batteries. Is that a correct? I would really appreciate your help. Thanks in advance.
PS: I have attached the circuit and my solution.
I am a newbee so please be kind
I have attached a DC circuit consisting of two opposing batteries and 3 resistors. The first step I took was to speculate on the direction of currents in both loops. I assumed the direction of conventional current for both loops, knowing full well that the maths will tell me if its correct by the operator in front of value. My results show that the middle branch has no volt drop across it as both currents are 180 degrees out of phase. The total voltage in the circuit is the sum of the two batteries. Is that a correct? I would really appreciate your help. Thanks in advance.
PS: I have attached the circuit and my solution.
I am a newbee so please be kind