TerryW
Gold Member
- 229
- 21
- Homework Statement
- MTW Ex 22.7(d)
- Relevant Equations
- (22.16h) - See attachment
I've come to a grinding halt with this and I can't see a way forward.
Can someone please take a look at what I've done so far and let me know if what I have done is OK and then if it is, give me a hint on how to proceed.
First up,
Is ## u \cdot \nabla \cdot T = u_\alpha T^{\alpha\beta}{}_{;\beta} ## ?
If it is, then from (22.16d)
##u_\alpha T^{\alpha\beta}{}_{;\beta} = u_{\alpha}(\rho u^\alpha u^\beta + (p - \zeta \theta)P^{\alpha \beta} -2\eta \sigma ^{\alpha \beta} +q^{\alpha} u^{\beta} +u^{\alpha} q^{\beta})_{;\beta}##
Working through the derivative and the projections, I reach
##u_\alpha T^{\alpha\beta}{}_{;\beta} = \rho \theta + u^{\beta}\rho_{;\beta} + u^i((p - \zeta \theta)_{;i} + \eta u^i(\frac{1}{3} \theta_{;i}) + u_i u^{\beta} q^i{}_{;\beta} = u_i q^i \theta -q^i{}_{;i}##
Where ##\theta = u^{\alpha}{}_{;\alpha}##
Is that OK?
RegardsTerryW
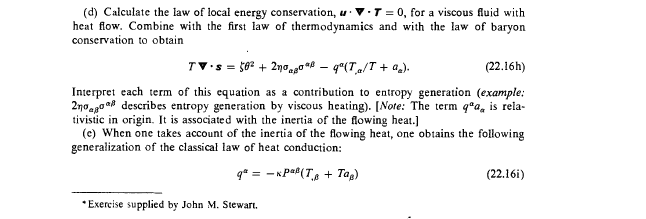
Can someone please take a look at what I've done so far and let me know if what I have done is OK and then if it is, give me a hint on how to proceed.
First up,
Is ## u \cdot \nabla \cdot T = u_\alpha T^{\alpha\beta}{}_{;\beta} ## ?
If it is, then from (22.16d)
##u_\alpha T^{\alpha\beta}{}_{;\beta} = u_{\alpha}(\rho u^\alpha u^\beta + (p - \zeta \theta)P^{\alpha \beta} -2\eta \sigma ^{\alpha \beta} +q^{\alpha} u^{\beta} +u^{\alpha} q^{\beta})_{;\beta}##
Working through the derivative and the projections, I reach
##u_\alpha T^{\alpha\beta}{}_{;\beta} = \rho \theta + u^{\beta}\rho_{;\beta} + u^i((p - \zeta \theta)_{;i} + \eta u^i(\frac{1}{3} \theta_{;i}) + u_i u^{\beta} q^i{}_{;\beta} = u_i q^i \theta -q^i{}_{;i}##
Where ##\theta = u^{\alpha}{}_{;\alpha}##
Is that OK?
RegardsTerryW
Last edited by a moderator: