Is the Friction Force Affected by an Inclined Force?

[Alex126]

Homework Statement

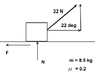
A block of mass m1 (8.5 kg) lies on a flat (non-incline) plane, with friction coefficient μ (0.2). It is pulled by a force F (32 N) that has makes an angle α (22°) with the plane. Determine:
- Acceleration
- After how much time t the body will have a velocity v = 1.2 m/s2

Homework Equations

F = m*a

The Attempt at a Solution

The doubt I have is in regards to what component of the force F we should consider. Here's a drawing:

I know there is also a Weight force pointing down, and a Normal force pointing up; I omitted them, as they shouldn't matter.

First, I need to write the forces on the body, and separate those on the X axis from those on the Y axis. I'll choose +Y going up, and +X going right.

X. [Friction] + [Force F_X] = m*a
Y. [Weight] + [Normal] + [Force F_Y] = 0 (since there is no vertical movement)

So here's the two stupid questions that I have.

Q1: Friction force = [coefficient] * [weight force_Y] ? I would have to say so, but for some reason in my mind now I have a doubt that it might be:
Friction force = [coefficient] * [weight force] * [cos (α)]

In other words, I don't know if I should take into consideration the fact that the force is "inclined" or not. My guess would be not...but my brain refuses to cooperate here, so please just give me the correct answer since I'll never get it on my own.

So, it's either A or B:
A. Friction force = 0.2*8.5*9.81 = 16.7
B. Friction force = 0.2*8.5*9.81* cos (22°) = 15.5

Q2: assuming we know the correct Friction force, now we need to find the acceleration. Obviously I'll be using the equation on the X axis, but I need Force F_X, which is the X-axis component of Force F. Correct?

If so, then I would say that Force F_X = Force F * cos (α)
That's because of this triangle here:

This sounds obvious and straight-forward to me, but I need confirmation please.

So at the end it would be:
a = (-Friction + Force F_X) / (m)
a = (-16.7 + 32*cos (22°) ) / (8.5)
OR
a = (-15.5 + 32*cos (22°) ) / (8.5)

Q3: do the forces on the Y axis really = 0 (= no motion) ? I would assume so, but here's the thing. If without Force F we have that Weight + Normal = 0, then why is it that with +Force F we still have = 0? If I had to guess I would say that it's because one between Weight and Normal goes down by -Force F, and since Weight is fixed, then the Normal force of the plane is actually lower by -Force F once the Force F is applied. Is this correct?

 

[Arman777]

Could you use latex or at least sembols.Its really hard to read

 

[Vector1962]

May I suggest you draw a sketch that labels all the forces? The sketches you have made are close, but are missing at least one force. It is very important to start with a nice sketch that labels ALL the forces.

 

[Vector1962]

Something like this...

 

[haruspex]

Friction force = [coefficient] * [weight force_Y] ? I would have to say so, but for some reason in my mind now I have a doubt that it might be:
Friction force = [coefficient] * [weight force] * [cos (α)]

Neither. What equations have you been taught regarding frictional forces? (Should be listed under relevant equations.)

Force F_X = Force F * cos (α)

Yes.

Weight force pointing down, and a Normal force pointing up; I omitted them, as they shouldn't matter.

They matter.

do the forces on the Y axis really = 0 (= no motion) ?

Yes.

the Normal force of the plane is actually lower by -Force F once the Force F is applied.

Not quite. Stick to vertical components.

 

[haruspex]

velocity v = 1.2 m/s2

I assume you mean m/s.

 

[Alex126]

I assume you mean m/s.

Yea, that was it, my bad >_<

Neither. What equations have you been taught regarding frictional forces? (Should be listed under relevant equations.)

We've been taught that friction = [weight component on the Y axis]*coefficient, but that was in slightly different problems where there was a block on an incline plane.

It might have also been friction = [Normal force]*coefficient, which I'm starting to believe might be the case due to the next quote.

They matter.

#Yforcesmatter

I thought they didn't matter because the Weight force was nullified by the Normal force. Can you elaborate as to why they matter?

Not quite. Stick to vertical components.

Oh, I see, I see. Let me try this again :D

the Normal force of the plane is actually lower by -Force F_Y once the Force F is applied.

So, since you mentioned that neither [Weight]*coefficient, nor [Weight]*coefficient*cos (22°) is correct, my next guess (I'm trying to read between the lines since nobody gave the direct answer) would be that friction force = normal*coefficient. So...(drumroll)

Friction force = ( [Weight]-[Force F_Y] ) * coefficient
(Where [Weight]-[Force F_Y] = "new" Normal force after Force F is applied)

Better, worse, or just as wrong? :D

 

[Alex126]

Hello?

 

[Vector1962]

You said it right, the friction force F_f = μN. You find N by ∑F_y (generally speaking).

 

[Alex126]

Ok, that's better. Thanks.