Is the length of the arm r in a polar coordinate a function of the angle?

[Leo Liu]

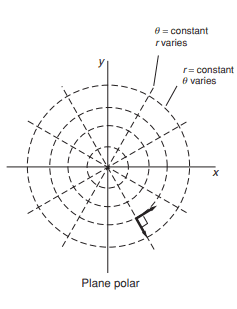
My textbook says $\vec r (\theta) = r \hat r (\theta)$, where $\hat r (\theta)$ is the terminal arm (a position vector in some sense). It can be seen that both $\vec r (\theta)$ and $\hat r (\theta)$ are function of $\theta$; whereas, the length of the vector $r$ is not. I understand that the unit vector r is a function of the angle because the direction of the arm is changing. However, I would like to know why the authors did not mention whether $r$ is a function of $\theta$. Thank you in advance :).

 

[Delta2]

$r$ is to $\theta$ what $x$ is to $y$ in a cartesian coordinate system. They are independent coordinates. They can be related only if you try to describe a curve, for example the curve of a spiral $r=a\theta$

However the unit vectors $\hat r,\hat\theta$ depend on $\theta$ while in a cartesian coordinate system the unit vectors $\hat x,\hat y,\hat z$ are constant and independent of the coordinates $x,y,z$. This crucial subtlety is the cause of many errors by students when working with polar coordinates.

 

[Ibix]

However, I would like to know why the authors did not mention whether $r$ is a function of $\theta$. Thank you in advance :).

Does $r$, the distance from the origin, change if you change only $\theta$?

 

[FactChecker]

You must be careful about what the different variables and symbols mean in the diagram. $r$ is not a vector. In the diagram, $r$ is the numerical distance between the origin and the point at the end of the vector $\vec r$. $\hat r(\theta)$ is the unit vector in the direction at angle $\theta$.

 

[PeroK]

My textbook says $\vec r (\theta) = r \hat r (\theta)$,

This is slightly inconsistent. $\vec r$ is a function of $r$ as well as $\theta$:
$$\vec r (r, \theta) = r \hat r (\theta)$$
Compare this with Cartesian coordinates:
$$\vec r (x, y) = x \hat x + y \hat y$$

 

[FactChecker]

However, I would like to know why the authors did not mention whether $r$ is a function of $\theta$. Thank you in advance :).
View attachment 266039

It is hard to say what is a function of what. The diagram shows one possibility is the radius line, where $\theta$ is constant and yet $r$ varies. In that case, $r$ is not a function of $\theta$. The notation of the equation $\vec r (\theta) = r\hat r (\theta)$ implies that, in the example of this equation, $r$ is a constant and is not a function of $\theta$. Since $r$ is a constant, the vector $\vec r (\theta)$ does not need to be considered a function of $r$.

 

[Leo Liu]

Does $r$, the distance from the origin, change if you change only $\theta$?

Probably not. But it does change if r is related to theta.

 

[Leo Liu]

$r$ is to $\theta$ what $x$ is to $y$ in a cartesian coordinate system. They are independent coordinates. They can be related only if you try to describe a curve, for example the curve of a spiral $r=a\theta$

However the unit vectors $\hat r,\hat\theta$ depend on $\theta$ while in a cartesian coordinate system the unit vectors $\hat x,\hat y,\hat z$ are constant and independent of the coordinates $x,y,z$. This crucial subtlety is the cause of many errors by students when working with polar coordinates.

Your explanation is very succinct, thank you.

 

[PeroK]

Probably not. But it does change if r is related to theta.

If $r$ is a function of $\theta$, then that describes a curve in the plane, in the same way that $y$ as a function of $x$ describes a curve.

You must distinguish that from the use of $r, \theta$ as independent coordinates.

 

[rude man]

$\hat {\bf r}$ is not a function of $\hat {\bf \theta}$. $\hat {\bf r}$ is as independent of $\hat {\bf \theta}$ as unit vector $\hat {\bf i}$ is to $\hat {\bf j}$.

 

[Leo Liu]

$\hat {\bf r}$ is not a function of $\hat {\bf \theta}$. $\hat {\bf r}$ is as independent of $\hat {\bf \theta}$ as unit vector $\hat {\bf i}$ is to $\hat {\bf j}$.

$\hat r$ is not a function of $\hat \theta$, yet it is a function of $\theta$.

 

[PeroK]

$\hat {\bf r}$ is not a function of $\hat {\bf \theta}$. $\hat {\bf r}$ is as independent of $\hat {\bf \theta}$ as unit vector $\hat {\bf i}$ is to $\hat {\bf j}$.

It's not clear in what sense those statements are true.

 

[vanhees71]

Let's use Cartesian basis vectors to describe the orthonormalized basis vectors referring to the polar coordinates, $(r,\varphi)$. The position vector in terms of polar coordinates then reads
$$\vec{r}=\vec{r}(r,\varphi)=r (\cos \varphi,\sin \varphi).$$
The (normalized) tangent vectors to the coordinate lines are
$$\hat{r}=\partial_r \vec{r}/|\partial_r \vec{r}|=(\cos \varphi,\sin \varphi)$$
and
$$\hat{\varphi}=\partial_{\varphi} \vec{r}/|\partial_{\varphi} \vec{r}|=(-\sin \varphi,\cos \varphi).$$
Indeed these vectors depend on the polar angle $\varphi$. It's also obvious when depicting the coordinate lines and the unit tangent vectors along them.

 

[rude man]

$\hat r$ is not a function of $\hat \theta$, yet it is a function of $\theta$.

How about the equation r = a? r not a function of $\theta$.

 

[Ibix]

How about the equation r = a? r not a function of $\theta$.

Note that $\hat r$ is a unit vector at the position identified by $r, \theta$. @Leo Liu is talking about $\hat r$, while you seem to be talking about $r$.

 

[Leo Liu]

How about the equation r = a? r not a function of $\theta$.

$$\begin{cases}
\hat r=\hat i \cos \theta + \hat i \sin \theta\\
\hat \theta = -\hat i \sin \theta + \hat j \cos \theta
\end{cases}$$

 

[rude man]

Yes that relates polar unit vectors to cartesian unit vectors.

But sticking to just the polar coordinates, $\hat {\bf r}$ is not a function of $\hat {\bf \theta}$.

A vector in polar coordinates is $\bf f = \bf f_r(r,\theta) \hat {\bf r} + f_\theta(r,\theta) \hat {\bf \theta}$.

If $\hat {\bf r} = \hat {\bf r}(\theta)$ then the two terms above could not be independent of each other.

Maybe we're talking different things. Or maybe I'm just missing something.

 

[weirdoguy]

But sticking to just the polar coordinates, is not a function of $\hat{\theta}$.

Yes, but did anyone said otherwise? It is not function of $\hat{\theta}$ but it is a function of angle $\theta$ (without 'hat') because it points in different directions depending on that angle. The same goes with $\hat{\theta}$. That's why formulas for velocity and acceleration are much more messier in polar coordinates.

 

[PeroK]

Yes that relates polar unit vectors to cartesian unit vectors.

But sticking to just the polar coordinates, $\hat {\bf r}$ is not a function of $\hat {\bf \theta}$.

On the contrary, we have:

$$\hat {\bf r} =
\begin{pmatrix} \cos \theta\\ \sin \theta \end{pmatrix} = \begin{bmatrix}

0 & 1 \\
-1 & 0 \\
\end{bmatrix}
\
\begin{pmatrix} -\sin \theta \\ \cos \theta \end{pmatrix}

= \begin{bmatrix}

0 & 1 \\
-1 & 0 \\
\end{bmatrix}
\
\hat {\bf \theta}
$$

And a linear mapping is, by definition, a function.

 

[Ibix]

Or maybe I'm just missing something.

You seem to be missing the distinction between the coordinates $r,\theta$ and the basis vectors $\hat r$ and $\hat \theta$.

$r=\sqrt{x^2+y^2}$ certainly is independent of $\theta$. However, to insist that $\hat r$ is independent of $\theta$ is to insist that every radial vector is parallel to every other radial vector (for example, one pointing to 12 o'clock and one pointing to 3 o'clock). That's obviously wrong.

 

[vanhees71]

How about the equation r = a? r not a function of $\theta$.

Sure, it's a function of $\theta$, namely $r(\theta)=a=\text{const}$. It describes a circle around the origin of the polar coordinate system with radius $a$.

 

[vanhees71]

You seem to be missing the distinction between the coordinates $r,\theta$ and the basis vectors $\hat r$ and $\hat \theta$.

$r=\sqrt{x^2+y^2}$ certainly is independent of $\theta$. However, to insist that $\hat r$ is independent of $\theta$ is to insist that every radial vector is parallel to every other radial vector (for example, one pointing to 12 o'clock and one pointing to 3 o'clock). That's obviously wrong.

$\hat{r}$ is the unit vector in radial direction and thus of course depends on $\theta$. Without specifying $\theta$ it's not defined to begin with. In curvilinear coordinate systems the basis vectors often depend on the location they refer to. In the case of plane polar coordinates, the orthonormalized basis is
$$\hat{r}=(\cos \theta,\sin \theta), \quad \hat{\theta}=(-\sin \theta,\cos \theta),$$
expressed in terms of the usual Cartesian basis system the polar coordinates are defined in.

 

[rude man]

Yes, but did anyone said otherwise? It is not function of $\hat{\theta}$ but it is a function of angle $\theta$ (without 'hat') because it points in different directions depending on that angle. The same goes with $\hat{\theta}$. That's why formulas for velocity and acceleration are much more messier in polar coordinates.

Formulas for velocity and acceleration are messier in cylindrical coordinates because the unit vectors are time-dependent.

 

[weirdoguy]

Yes, but that's because they depend on $\theta$ which is usually a function of time.

 

[Ibix]

Formulas for velocity and acceleration are messier in cylindrical coordinates because the unit vectors are time-dependent.

The unit vectors aren't time dependent for a stationary object, so the time dependence for a moving object clearly comes from the time variation of position.

 

[PeroK]

Formulas for velocity and acceleration are messier in cylindrical coordinates because the unit vectors are time-dependent.

Does that mean that the polar unit vectors will be different tomorrow?

 

[rude man]

Yes, but that's because they depend on $\theta$ which is usually a function of time.

Yes that's correct. At least they can be.
In fact, $d\hat{\bf r}/dt = (d\theta/dt)~ \hat{\bf\theta}$ and
$d\hat{\bf\theta}/dt = - d\theta/dt ~ \hat{\bf r}$.

But expressions for velocity and acceleration also have terms in them not a function of $\theta$ or $\hat{ \theta}$.

For example, acceleration $\bf a$ is
$\bf a = (d^2r/dt^2~ -... ~) ~ \hat{ \bf r} + ... +(d^2z/dt^2) \hat {\bf z}.$

 

[vanhees71]

Well, for a moving object you have in polar coordinates $r=r(t)$ and $\theta=\theta(t)$. For the position vector we have
$$\vec{r}=r \hat{r} \; \Rightarrow \; \vec{v}=\text{d}_t \vec{r} = \dot{r} \hat{r} + r \mathrm{d}_t \hat{r} = \dot{r} \hat{r} + r \dot{\theta} \partial_{\theta} \hat{r}=\dot{r} \hat{r} + r \dot{\theta} \hat{\theta},$$
where I've used that
$$\partial_{r} \hat{r}=0, \quad \partial_{\theta} \hat{r}=\hat{\theta}.$$
Further we need
$$\partial_{r} \hat{\theta}=0, \quad \partial_{\theta} \hat{\theta}=-\hat{r}.$$
With this we get
$$\mathrm{d}_t^2 \vec{r}=\mathrm{d}_t \vec{v} = \ddot{r} \hat{r} + 2 \dot{r} \dot{\theta} \hat{\theta} + r \ddot{\theta} \hat{\theta} -r \dot{\theta}^2 \hat{r}=(\ddot{r}-r \dot{\theta}^2) \hat{r} + (r \ddot{\theta} +2 \dot{r} \dot{\theta}) \hat{\theta}.$$