mcastillo356
Gold Member
- 658
- 361
- TL;DR
- I am not sure to see the expected bijection between the rationals and the natural numbers
Hi, PF
Theorem
The set ##\mathbb{Q}## of the rational numbers is countably infinite.
Proof
The rational numbers are arranged thus
$$\cfrac{0}{1},\,\cfrac{1}{1},\,\cfrac{-1}{1},\,\cfrac{1}{2},\,\cfrac{-1}{2},\,\cfrac{2}{1},\,\cfrac{-2}{1},\,\cfrac{1}{3},\,\cfrac{2}{3},\,\cfrac{-1}{3},\,\cfrac{-2}{3},\,\cfrac{3}{1},\,\cfrac{3}{2},\,\cfrac{-3}{1},\,\cfrac{-3}{2},\,\cfrac{1}{4},\,\cfrac{3}{4},\,\cfrac{-1}{4},\,\cfrac{-3}{4},\,\cfrac{4}{1},\,\cfrac{4}{3},\,\cfrac{-4}{1},\,\cfrac{-4}{3}\cdots{}$$
It is clear that every rational number will appear somewhere in this list.
Thus it is possible to set up a bijection between each rational number and its position in the list, which is an element of ##\mathbb{N}##
##\blacksquare##
Attempt
Impossible to arrange any bijection, except if it implicitly recalls Cantor's comparison between rational and natural numbers, this is:

Greetings, Marcos
Theorem
The set ##\mathbb{Q}## of the rational numbers is countably infinite.
Proof
The rational numbers are arranged thus
$$\cfrac{0}{1},\,\cfrac{1}{1},\,\cfrac{-1}{1},\,\cfrac{1}{2},\,\cfrac{-1}{2},\,\cfrac{2}{1},\,\cfrac{-2}{1},\,\cfrac{1}{3},\,\cfrac{2}{3},\,\cfrac{-1}{3},\,\cfrac{-2}{3},\,\cfrac{3}{1},\,\cfrac{3}{2},\,\cfrac{-3}{1},\,\cfrac{-3}{2},\,\cfrac{1}{4},\,\cfrac{3}{4},\,\cfrac{-1}{4},\,\cfrac{-3}{4},\,\cfrac{4}{1},\,\cfrac{4}{3},\,\cfrac{-4}{1},\,\cfrac{-4}{3}\cdots{}$$
It is clear that every rational number will appear somewhere in this list.
Thus it is possible to set up a bijection between each rational number and its position in the list, which is an element of ##\mathbb{N}##
##\blacksquare##
Attempt
Impossible to arrange any bijection, except if it implicitly recalls Cantor's comparison between rational and natural numbers, this is:

Greetings, Marcos
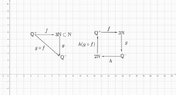
 . My target, anyhow, is ##\mathbb{Q}\rightarrow{\mathbb{N}}##
. My target, anyhow, is ##\mathbb{Q}\rightarrow{\mathbb{N}}##