Thanks for the clarification! I happen to agree with what you highlight in red.
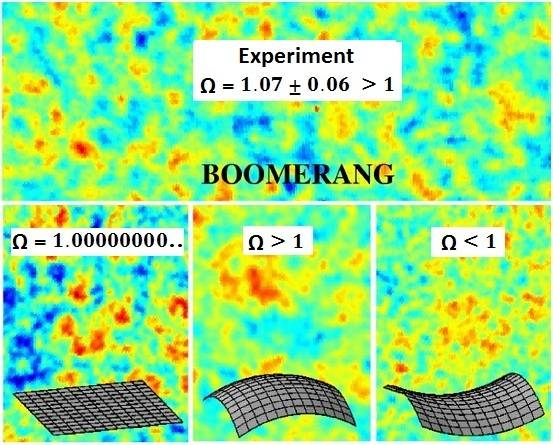
As I recall from the WMAP5 report, they do not even claim the
observable universe is flat. They use words like "nearly flat". The data is consistent (within uncertainty bounds) with the perfectly flat model. And also it is consistent with a overall slightly curved model.
The Cornell "Ask an astronomer" site is primarily for pre-college young people, I think. Some of the language is oversimplified or not carefully enough qualified, so you have to be cautious about taking it literally sometimes. What you quoted is a case of that:
So when we say "WMAP provides strong evidence that the universe is flat", we really mean "WMAP provides strong evidence that the observable universe is flat".
curious.astro.cornell.edu/question.php?number=171
WMAP does NOT provide strong evidence that the observable universe is EXACTLY flat.
It provides wonderfully strong evidence that Omega is in the range
0.9916 < Omega < 1.0133 (talking about the universe as a whole, assuming uniformity)
And what that translates to, in the picture of a very large balloon that looks flat to creatures living on it, is that if the curvature is at the upper limit you have a circumference of 750 billion light years (again the universe as a whole.)
That is one way of gauging the "near flatness". When you say "nearly" you suppose some way of quantifying curvedness. Most people don't grok Omega. It doesn't do anything for them to say "within one percent of unity". So you can translate that into the large balloon picture and say that the most distant matter is AT LEAST 375 billion LY away (half the circumference).
The radius of the portion we can now observe is some 45 billion LY. So the whole balloon is AT LEAST ten times bigger than what we can see---in the vague way that 375 is bigger than 45. The most distant stuff is an order of magnitude (factor of 10) farther than the most distant stuff we can see.
Or you could talk in terms of the "RADIUS OF CURVATURE" of the local patch of universe we currently see. It is one way a mathematician might quantify curvedness. Divide the circumference of 750 by 2 pi. Is that about 120?
I think I'm just repeating, but maybe that doesn't hurt. We don't have, in our common everyday language, good ways to talk about degrees of curvedness. But to give an honest account of what is known (WMAP and also BAO and SN data) we have to have a way. We can't just say "flat" and give the listener the idea of EXACTLY flat. We have to say nearly, and that supposed a concept of amount of flatness or curvedness.
If you like the idea of a "radius of curvature" then 2010 WMAP report says that RoC of the patch of universe we can see is, with 95% confidence, at least 120 billion LY
that is the radius of the fitting hypersphere, if the observable patch were laid on the 3D "surface" of a fitting 4D hypersphere.