darkfeffy
- 17
- 0
Hi,
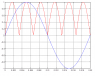
I wish to obtain the Fourier series of the signal in red (please see attached figure fig1_sine_plots.png). Basically, it is a full-wave rectified 3f sinusoid, where f = 50Hz. The blue signal represents a sinusoid with frequency f = 50Hz.
In the following equations (please see attached figure fig2_equations.png), “T” represents the period of the signal in blue and w0 is the angular frequency of the signal in blue.
One can only arrive at the correct representation of the a.c. (alternating current) part of the signal if the values of n are even and multiples of 3 (i.e. n = 6, 12, 18, etc.). Well, to be technically accurate, it suffices for n to be a multiple of 3, because the odd multiples will each have an amplitude of 0.
So, I have a problem at this point. I have most probably forgotten some of the theory behind the Fourier Series, but can someone explain why the values of n need to multiples of 3? According to the equations above (please see attachment fig2_equations), there is no restriction as to the different positive values that n can have. Why can’t n = 4? Or n = 5? Or n = 8? Also, why can’t n be less than 3?
Thanks in advance.
I wish to obtain the Fourier series of the signal in red (please see attached figure fig1_sine_plots.png). Basically, it is a full-wave rectified 3f sinusoid, where f = 50Hz. The blue signal represents a sinusoid with frequency f = 50Hz.
In the following equations (please see attached figure fig2_equations.png), “T” represents the period of the signal in blue and w0 is the angular frequency of the signal in blue.
One can only arrive at the correct representation of the a.c. (alternating current) part of the signal if the values of n are even and multiples of 3 (i.e. n = 6, 12, 18, etc.). Well, to be technically accurate, it suffices for n to be a multiple of 3, because the odd multiples will each have an amplitude of 0.
So, I have a problem at this point. I have most probably forgotten some of the theory behind the Fourier Series, but can someone explain why the values of n need to multiples of 3? According to the equations above (please see attachment fig2_equations), there is no restriction as to the different positive values that n can have. Why can’t n = 4? Or n = 5? Or n = 8? Also, why can’t n be less than 3?
Thanks in advance.