It's not electrical, it's purely mathematical

[pixel01]

Hi all,

I posted this thread here and it was removed to electrical box (https://www.physicsforums.com/showthread.php?t=169778). In fact it is not an electrical. I hope this time it can be solved.

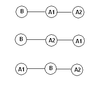
There is a battery (B) and n bulbs (A1, A2... An). Now that I have to make a circuit from the battery to all the bulbs. There should be no loops. You can make it in series or trees, but no loops. The question is: ' how many ways to make a circuit are there? '.
Here I draw a picture illustrating the case n=2. Because there are only 3 knots so there's no tree.

Thanks.

 

[lalbatros]

I think the position of the battery does not matter.
You just need to calculate to number of connected trees that can be done with n bulbs.
Try recusivity.