Jones Vector of Linear Polarization

[iScience]

Hi, I understand that the α in the form below refers to angle of E-vector to the horizontal.

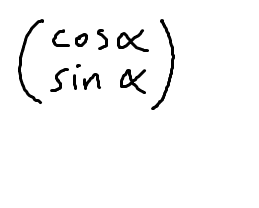
and that a jones vector should be represented this way:

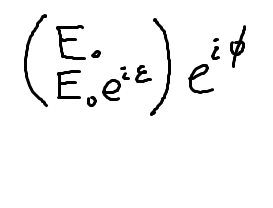
I tried to represent the linearly polarized sin & cos form in the jones vector form

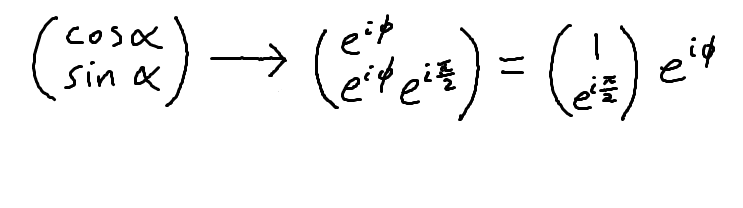I know I'm doing something wrong because a linearly polarized light should have no phase delays between x & y. I'm just getting my space and time domains mixed up.Thanks

 

[iScience]

Mainly the reason I am confused is because in my book it gives this form for linearly polarized light:

$$\vec{E}=(\hat{i}E_{0(x)}+\hat{j}E_{0(y)})cos(kz-\omega t)$$

the two components being cosine makes sense because 0 phase difference.

but if i write that in matrix form, shouldn't i also have two cosines, not one cosine and one sine?

 

[Andy Resnick]

If I understand your first post, you are on the right track- linearly polarized light with polarization oriented and angle 'α' from the x-axis is indeed written as you say, if you are using linear basis states. The use of 'ε' in your second image makes me wonder if you are now trying to write the Jones vector for elliptically polarized light (with ellipticity ε), which using linear basis states is:

[E_x, E_y] = [cos ε, i sin ε]

which kinda-sorta looks like it can be converted into what you showed.

As for your second post, I am guessing that E_x and E_y are the x- and y- components of E, which again result in E = [E_x, E_y] = E_0 [cos α, sin α] as before. The cos(kz-ωt) refers to the 'wave part', not the polarization, which is simply the direction of E.

Does this help?