miikaelf
- 2
- 0
Hi everbody!
This has been bugging me for quite some time now, so I would be forever grateful and challenge you to think about this.
According to the Wikipedia (and phyiscs textbooks),
" Since the assumption is that the particles move in random directions, we will have to conclude that if we divide the velocity vectors of all particles in three mutually perpendicular directions, the average value along each direction must be same. (This does not mean that each particle always travel in 45 degrees to the coordinate axes.)
Therefore the velocity vector Vx2=V2/3.
"
http://en.wikipedia.org/wiki/Kinetic_theory
My beef is with how they explain deriving the component vectors.
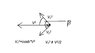
The velocity vectors (or their squares) are *vectors* and not scalar values, thus should be added and subtracted as vectors (see attachment).
This means that they *should NOT* be simply divided by three, but be dealt with as vectors.
No physics text I have come across so far has adressed this, so
a) Is this correct (I presume it is, otherwise my faith in humanity and physics will crumble to dust)
and
b) Why can we treat them as scalar values?
Thank you and have a happy new year!
This has been bugging me for quite some time now, so I would be forever grateful and challenge you to think about this.
According to the Wikipedia (and phyiscs textbooks),
" Since the assumption is that the particles move in random directions, we will have to conclude that if we divide the velocity vectors of all particles in three mutually perpendicular directions, the average value along each direction must be same. (This does not mean that each particle always travel in 45 degrees to the coordinate axes.)
Therefore the velocity vector Vx2=V2/3.
"
http://en.wikipedia.org/wiki/Kinetic_theory
My beef is with how they explain deriving the component vectors.
The velocity vectors (or their squares) are *vectors* and not scalar values, thus should be added and subtracted as vectors (see attachment).
This means that they *should NOT* be simply divided by three, but be dealt with as vectors.
No physics text I have come across so far has adressed this, so
a) Is this correct (I presume it is, otherwise my faith in humanity and physics will crumble to dust)
and
b) Why can we treat them as scalar values?
Thank you and have a happy new year!