Kirchhoff's Rules: Solving Homework Questions on Circuit Currents

[Roze]

Homework Statement

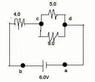
Find the currents in the circuit shown in the figure attached.

Homework Equations

I actually have the solution worked out but I don't understand why something was done. So they chose to travel the bottom loop and the top loop clockwise in both cases. So they set up the equation:

sum deltaV = Vbattery + V4.0 + V9.0

What I don't understand is why they chose to add the V9.0, rather than the V5.0, or both. How do I know that this is the resistor you use for this equation? I understand you're traveling the loop clockwise, but I don't understand why the 9.0 resistor is used rather than the 5.0 or their equivalent resistance.

Also, when they plug in the numbers for this equation they give:

sum deltaV = 6.0V -4.0I2 - 9.0I3

Why are the 4.0 and 9.0 components negative? Is it because they're on the other side of the battery?

Similarly, for the top loop they give the equation:

sum deltaV = -5.0I2 + 9.0I3

Why in this case is the 5.0 negative but the 9.0 positive?

The Attempt at a Solution

See above.

Apologies for the terrible picture.

 

[Chi Meson]

You have to have the concept of a "voltage drop" across a resistor. As the current flows, the flowing charges have more energy on the left side of the resistors (in this image) than they do on the right sides. It helps to draw arrows above each resistor to show the direction that current (conventional current, I) is going. THis way you can tell if you you are dropping voltage ("negative," is going with the arrow) or gaining voltage (going against the arrow).

Of course you gain voltage when you go "with" the current through a battery, but you drop voltage when you go with the current through a resistor.

So in the second loop, as you go clockwise, you go with the current through one resistor, but against the current through the other resistor.

And the first loop simply chose the 9 ohm resistor randomly. You have to pick a single path in each loop. The problem would work just as well if they had chosen the 5 ohm resistor.

 

[Chi Meson]

sum deltaV = 6.0V -4.0I2 - 9.0I3

sum deltaV = -5.0I2 + 9.0I3

One of these is incorrect. I am assuming that the current through the 4 ohm resistor is "I1." The current can't be the same through both 4 and 5.

You need a third equation (junction rule) which simply says I1 = I2 + I3.

What I don't understand is, why use Kirchoff's rules for this simple circuit? Just for practice? It would be easier to find the equivalent resistance, then the total current, then find the proportional split of the current through the parallel.