Lagrangian Equation with Generalized Force term

[KT KIM]

In basic level classical mechanics I've known so far
The Lagrangian Equation is
Like this

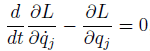
But in the little deeper references, they covers Lagrangian Equation is
Like this

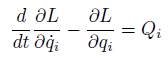
Qi is Generalized force, and Qi also contains frictions that's what reference says
But I still can't grasp.

What is the difference between these two equation, and What Is "Generalized Force" ?

 

[ChrisVer]

I guess this link can help you:
https://en.wikipedia.org/wiki/Virtual_work

 

[twist.1995]

The generalized forces can be both conservative and non-conservative. The gravitational force of attraction, the buoyancy force, the spring force, the electric and magnetic forces (and electromagnetic time invariant forces) are conservative and they also have the potential function associated with the vector field $\vec F$ : $- \nabla \Phi = \vec F$. The non-conservative are the forces that do not store the energy in the field. The examples of these forces are the friction force, the air resistance, the damping force, the viscous force, the drag force, the time-varying electromagnetic fields, etc. The total work done on a system will be $W=W_{cons}+W_{non-cons} = KE_{f} - KE_{i} = -\delta PE$. The generalized force can be found as: $f_{i}=f_{cons}+f_{non-cons}$. If you have already included the conservative forces in your Lagrangian expression, for example, you found the potentials of the given vector fields, your generalized forces will be the non-conservative forces.