Lagrangian for pendulum with moving support

[Decimal]

Homework Statement

[/B]
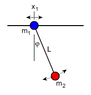
In a homogeneous gravity field with uniform gravitational acceleration g,
a pointmass m1 can slide without friction along a horizontal wire. The mass m1 is the pivot point of a
pendulum formed by a massless bar of constant length L, at the end of which a
second pointmass m2 is attached. m2 can oscillate within the plane. I included a drawing.

Find the equations of motion for this system

Homework Equations

[/B]
Lagrangian
$$ \mathcal{L} = T - V $$

Lagrange equations
$$\frac {d} {dt} (\frac {d\mathcal{L}} {\dot {dq_i}}) - (\frac {d\mathcal{L}} {dq_i}) = 0 $$

Conjugate momenta
$$p_i = (\frac {d\mathcal{L}} {\dot {dq_i}}) $$
$$\dot {p_i} = (\frac {d\mathcal{L}} {dq_i}) $$

The Attempt at a Solution

[/B]
First I computed the kinetic energy and potential energy. $$ T = \frac {1} {2} \dot {x_1}^2*(m_1+m_2) + m \dot {x_1} \dot {\phi} L cos(\phi) + \frac {1} {2} m_2 L^2 \dot {\phi}^2 $$ and $$ V = -m*g*L*cos(\phi) $$ Now I can calculate the Lagrangian: $$ \mathcal{L} = \frac {1} {2} \dot {x_1}^2*(m_1+m_2) + m \dot {x_1} \dot {\phi} L cos(\phi) + \frac {1} {2} m_2 L^2 \dot {\phi}^2 - -m*g*L*cos(\phi) $$ From this I can calculate the conjugate momenta, which then equal: $$ p_{x1} = \dot {x_1} (m1+m2) + m_2 \dot {\phi} L cos(\phi) $$ $$ p_\phi = m_2 L^2 \dot {\phi} + m_2 \dot {x_1} L cos(\phi) $$ Now using the lagrange equations I find the following equations of motion: $$ \ddot {x_1} (m1+m2) + m_2 \ddot {\phi} L cos(\phi) - m_2 \dot {\phi}^2 L sin(\phi) = 0 $$ $$ m_2 L^2 \ddot {\phi} + m_2 \ddot {x_1} L cos(\phi) - m_2 * \dot {x_1} \dot {\phi} L sin(\phi) = -m_2 g L sin(\phi) $$ Now straight up solving these equations for $\ddot {x_1}$ and $\ddot {\phi}$ will take quite a lot of work, so I was wondering whether there is an easier way to get the answer without solving this system directly. I feel like I should to do something with the fact that $\dot {p_{x1}} = 0$ so $p_{x1}$ is conserved. I am just not quite sure how I can use this. Help would be greatly appreciated!

Thanks!

 

[Dr.D]

It has been many years since I worked this problem, and I don't recall the result. However, I notice that you did not present anything about the kinematics of the system, but rather jumped straight into writing the energies. The kinematics is where things usually go wrong, in my experience as a teacher. I'd check that part before worrying about solving the differential equations. Time spent solving the wrong equations is utterly wasted.

 

[Decimal]

It has been many years since I worked this problem, and I don't recall the result. However, I notice that you did not present anything about the kinematics of the system, but rather jumped straight into writing the energies. The kinematics is where things usually go wrong, in my experience as a teacher. I'd check that part before worrying about solving the differential equations. Time spent solving the wrong equations is utterly wasted.

Thanks for the response, I assume by kinematics you mean the way in which I derived the velocities of the two point masses. The velocity of the first mass is just $\dot{x_1}$, for the second mass I first wrote down the position vector, expressed in cartesian coordinates: $$ \vec {r_2} = \begin{pmatrix} x_1 + L sin(\phi) \\ -L cos(\phi) \end{pmatrix} $$ Then the velocity will equal: $$ \vec {v_2} = \begin{pmatrix} \dot {x_1} + L cos(\phi) \dot {\phi} \\ L sin(\phi) \dot {\phi} \end{pmatrix} $$ and then $$ \vec {v_2}^2 = \dot {x_1}^2 + 2*\dot {x_1} L cos(\phi) \dot {\phi} + L^2 \dot {\phi}^2 $$ Now given that $$ T = \frac {1} {2} m_1 \vec {v_1}^2 + \frac {1} {2} m_2 \vec {v_2}^2 $$ I arrive at the expression for kinetic energy I mentioned in the original post.

 

[Dr.D]

That does indeed look OK for the kinematics, so I think you are safe there

You complained that it was going to be difficult to solve the coupled system (and so it is), but it remains difficult (not impossible) to solve the system if you fix the value of x1. The large amplitude pendulum requires elliptic integrals for the solution, and that is not trivial at all. When you compound the difficulty by adding another degree of freedom, we can hardly expect the solution to get simpler.

 

[Decimal]

Thanks a lot for the help! However it turns out I missed a bit of information about the problem. I was supposed to derive the equations that I found and then apply a first order approximation on the angles, which does simplify them quite a bit.

Thanks for the effort though!

 

[Dr.D]

To be sure, that is a major simplification! Glad you noticed that bit!