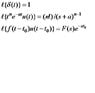Laplace Transform Proofs: Get Help Now

[smms25]

Hey, I have been studying differential equations a bit and was wanting some help on some proofs. There are 3 laplace transforms I would like proofs for. Not really sure where to get started or if someone could lead me to place that has these proofs I would greatly appreciate it. Thank you.

 

[HallsofIvy]

Have you tried just integrating?

The definition of the Laplace transform of f(x) is
$$\int_0^\infty e^{-sx}f(x)dx$$

The transform of the delta function is pretty close to trivial:
$$\int_0^\infty e^{-sx}\delta(x)dx= e^{0x}= 1$$

For $f(x)= x^ne^{ax}u(x)$ do repeated integration by parts letting $u= x^n$, $dv= e^{ax}u(x)$ until you have reduced the power of x to 0.

For $f(t-t_0)u(t-t_0)$ do the obvious substitution: let $v= t- t_0$.