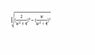You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Learn How to Manipulate a Formula to Find 1/(sqr(w^2+4)) in Simple Steps
- Thread starter greg997
- Start date
AI Thread Summary
The discussion focuses on manipulating the formula to achieve 1/(sqrt(w^2+4)). Participants clarify that the original equations are not equal, and one user suggests a corrected expression involving fractions. Hints are provided to guide the user in solving the problem, emphasizing the importance of showing initial attempts at manipulation. A misunderstanding about adding fractions versus multiplying numerators is acknowledged, leading to a realization of the mistake. The conversation highlights the need for careful application of mathematical rules to achieve the desired result.
Physics news on Phys.org
jack action
Science Advisor
- 3,496
- 9,706
The two equations are not equal. Just replace w by any value and you'll see that both equations give different answers.
Mentallic
Homework Helper
- 3,802
- 95
The best you can really get is:
\frac{\sqrt{4-w^2}}{w^2+4}
\frac{\sqrt{4-w^2}}{w^2+4}
Last edited:
Mentallic
Homework Helper
- 3,802
- 95
You must have made a typo. The expression should be,
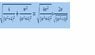
\sqrt{\left(\frac{2}{w^2+4}\right)^2+\left(\frac{w}{w^2+4}\right)^2}
\sqrt{\left(\frac{2}{w^2+4}\right)^2+\left(\frac{w}{w^2+4}\right)^2}
greg997
- 105
- 2
Mentallic said:You must have made a typo. The expression should be,
\sqrt{\left(\frac{2}{w^2+4}\right)^2+\left(\frac{w}{w^2+4}\right)^2}
Hmm, that's quite possible. Then how to get that solution?
Mentallic
Homework Helper
- 3,802
- 95
Well I can't just give you the answer, you need to show an attempt at solving the problem first.
But I can give you some hints, you can most certainly find the answer by using a combination of these rules:
\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}
\sqrt{a^2b}=|a|\sqrt{b} (the |a| means the positive of a, but remember that for any real number n, n2 is always positive).
\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}
\frac{\sqrt{a}}{a}=\frac{1}{\sqrt{a}}
Good luck!
But I can give you some hints, you can most certainly find the answer by using a combination of these rules:
\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}
\sqrt{a^2b}=|a|\sqrt{b} (the |a| means the positive of a, but remember that for any real number n, n2 is always positive).
\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}
\frac{\sqrt{a}}{a}=\frac{1}{\sqrt{a}}
Good luck!
Cyosis
Homework Helper
- 1,495
- 5
You're adding fractions, but you're multiplying numerators.
greg997
- 105
- 2
AAA, stupid me:) Thanks
Similar threads
- Replies
- 16
- Views
- 3K
- Replies
- 11
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 8
- Views
- 1K
- Replies
- 3
- Views
- 1K
- Replies
- 19
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 8
- Views
- 2K
- Replies
- 10
- Views
- 2K
- Replies
- 2
- Views
- 1K
Hot Threads
-
Geometry: Similar Shapes
- Started by paulb203
- Replies: 116
- Precalculus Mathematics Homework Help
-
Length of Diagonal
- Started by erobz
- Replies: 45
- Precalculus Mathematics Homework Help
-
Find integer points on this equation
- Started by littlemathquark
- Replies: 8
- Precalculus Mathematics Homework Help
-
[ASK] Trigonometric Inequality
- Started by Monoxdifly
- Replies: 6
- Precalculus Mathematics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math