dumplump
- 39
- 0
I have recently purchased this textbook. When I compare it to my class, I find that the exercises are of significantly higher difficulty. There are tricks to solving the problems that I never would have thought of because quite honestly I never learned them. For example the textbook, chapter on integration by parts, there is a problem that is solved by adding and subtracting 1 from the numerator.
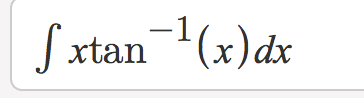
I did not know I could do that, and I was stuck until I plugged the problem into Symbolab.
Here is the property that is needed in order to solve, but I was not able to find the name of this property
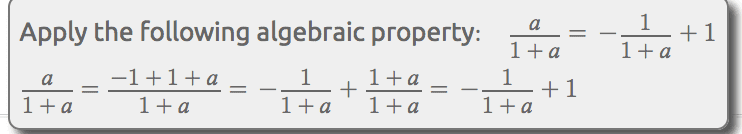
For those who have used this book, The Calculus 7 Louis Leithold, how did you overcome these difficulties? I have purchased Leithold's Before Calculus text as well. I feel that my previous textbook just was not sufficient because I did not see the following property above in the text, or should I say I do not remember it being in the text.
I did not know I could do that, and I was stuck until I plugged the problem into Symbolab.
Here is the property that is needed in order to solve, but I was not able to find the name of this property
For those who have used this book, The Calculus 7 Louis Leithold, how did you overcome these difficulties? I have purchased Leithold's Before Calculus text as well. I feel that my previous textbook just was not sufficient because I did not see the following property above in the text, or should I say I do not remember it being in the text.