relskhan
- 5
- 0
So I'm trying to model two particle interaction subject only to Lennard Jones potential. I have a specific potential I am using:
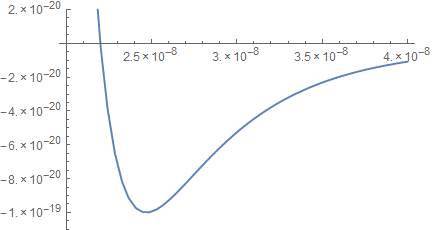
My problem is forcing the two particles into the potential well. I have the particles at a separation distance of 2.5*10-8. The way I interpret this potential is that I can set a total energy of -6.0*10-20 by giving the particles a Kinetic Energy of 3.95*10-20 (Where Total Energy TE=KE + U or KE = TE - U => KE = -6.0*10-20 +9.95*10-20 = 3.95*10-20 , the -9.95*10-20 comes from U(2.5*10-8).
To set the kinetic energy I'm using 1/2 m (v12+v22). And giving particle 1 an initial velocity equal to some factor of particle 2's velocity.
Unfortunately, this is still not working. So I am either interpreting the different energy requirements on the diagram wrong - or not calculating the velocity for the KE correctly. Any ideas??
My problem is forcing the two particles into the potential well. I have the particles at a separation distance of 2.5*10-8. The way I interpret this potential is that I can set a total energy of -6.0*10-20 by giving the particles a Kinetic Energy of 3.95*10-20 (Where Total Energy TE=KE + U or KE = TE - U => KE = -6.0*10-20 +9.95*10-20 = 3.95*10-20 , the -9.95*10-20 comes from U(2.5*10-8).
To set the kinetic energy I'm using 1/2 m (v12+v22). And giving particle 1 an initial velocity equal to some factor of particle 2's velocity.
Unfortunately, this is still not working. So I am either interpreting the different energy requirements on the diagram wrong - or not calculating the velocity for the KE correctly. Any ideas??