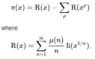I |Li(x) - pi(x)| goes to 0 under RH?

[nomadreid]

Extremely quick question:
According to http://mathworld.wolfram.com/PrimeNumberTheorem.html, the Riemann Hypothesis is equivalent to
|Li(x)-π(x)|≤ c(√x)*ln(x) for some constant c.
Am I correct that then c goes to 0 as x goes to infinity?
Does any expression exist (yet) for c?
Thanks.

 

[fresh_42]

Extremely quick question:
According to http://mathworld.wolfram.com/PrimeNumberTheorem.html, the Riemann Hypothesis is equivalent to
|Li(x)-π(x)|≤ c(√x)*ln(x) for some constant c.

Quick answer:

Am I correct that then c goes to 0 as x goes to infinity?

No. $c$ is a constant factor and goes nowhere. However, there are better approximations which may depend on x.

Does any expression exist (yet) for c?
Thanks.

Wikipedia has $c=\dfrac{1}{8\pi}$ found by L. Schoenfeld.

 

[nomadreid]

Super! Thanks, fresh_42

 

[mfb]

Wikipedia has $c=\dfrac{1}{8\pi}$ found by L. Schoenfeld.

For x>2657 (and only if the Riemann hypothesis is true, of course). Smaller values probably require a larger c, and we have to exclude x=1 of course.

 

[nomadreid]

Thanks for the precision, mfb.
I followed up on fresh_42 's remark

there are better approximations which may depend on x.

to find better approximations, and found one at one source that I have not been able to find elsewhere: the first entry on
https://www.quora.com/What-is-the-relationship-between-the-Riemann-Hypothesis-and-prime-numbers
gives an exact formula which depends on the zeros of the zeta function under the assumption that the RH is correct and p primes: via a Möbius tranformation of:

PS. After writing this, I noticed https://en.wikipedia.org/wiki/Prime-counting_function#Exact_form, which I presume is equivalent to the above.

 

[fresh_42]

For x>2657 (and only if the Riemann hypothesis is true, of course). Smaller values probably require a larger c, and we have to exclude x=1 of course.

As an add-on: This is standard for big-O notations, that they are only valid from a certain level on. E.g. the matrix exponent for 2 x 2 matrices is exactly $\log_27$ but there are better bounds for larger $n$, but it doesn't make the constant a variable.

 

[nomadreid]

After letting these answers ferment in my head for a while, I conclude that the answer to my implicit question about why we talk about approximations if there are exact formulas such as the one listed in the Wikipedia page

where μ(n) is the Möbius function, is that although this formula would be indeed exact (assuming RH), it is so tedious as to not be of much use even if we had an efficient method for producing non-trivial zeros, just as the brute-force counting is indeed an exact algorithm but of no use for large numbers, so that the approximations referred to are more important because they are reasonably tractable. That is, we sacrifice precision for speed. I hope this is an accurate representation?

 

[Clarkthomas36]

The Riemanm Hypothesis is basically a Fourier series representation of a function we have no way of describing long term properties of otherwise. Suppose I want to know roughly what the 10^10^10th prime number is for some futuristic encryption process. What does roughly mean? It means that I can get you in the ball park of the desired prime, using the prime number theorem, but I still need to get closer, but not exact. How would I do that? I could pretend I have the exact function, but in terms of other equations, maybe at first I only care about the average order/general growth form. That gets me pretty close but I need to make sure that I am not getting the next prime or the previous prime. I know the average growth order, but my actual prime counting function kinda oscillates around that growth order function. What if I use a sort of Fourier series representation, letting the waves cancel out when my average order is equal to the prime counting function, and adding up or down to take my average order function and correct it to look like the prime counting function? That would be what I needed, but how would I garentee I get the correct weights on my waves? How do I garentee that I choose the correct waves? It turns out that the Prime Counting Function can be shaped into another function purely by using algebra. Taking that new equation, and applying a special kind of Fourier transform to it gets us to the an expression including the zeta function?! Well look at that. Okay, but what are the weights? Well if we look at when 1/zeta is infinite, we can use the complex analysis to tease out the weights. So if we care about when 1/zeta is infinite, then we also care about when zeta is 0. All zeros and poles if the zeta function, including the trival zeros contribute to the approximation expression, and the more contributions we allow, the less it looks like an approximation. So as it appears, we can find the nth prime number by forming the approximation, and then just including enough terms. The difference from other prime solving methods is the computational complexity. Suppose I want to even prove that the numbers up at 10^10^10 are prime or not, let alone, tell if its the one I want? Well, a primality test requires I check my number against all the numbers which come before it. Considering the prime gaps at this height are very large in magnitude, ill be checking numbers all day...er all decade. Instead, I can just form the approximation out of these important points, and I know/suspect where they all are, so as long as I just look there, I can ignore the rest of the function, also if I know the zeros, and have them stored, then I never have to find them again. It turns out to be very useful/faster to use the zeta function to find information about the primes. I don't even need an infinite number of zeros, because I don't need a perfect approximation, only good enough that my appoximation is not changing much anymore for me to be confident.