Light incident on a sphere, focused at a distance ##2R##

[lorenz0]

Homework Statement

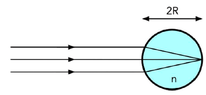
A solid sphere with index of refraction $n$ and radius $R$, placed in air, is illuminated by a beam of light coming from a source at a great distance, which is focused on the bottom surface of the sphere. Determine the value of $n$.

Relevant Equations

$\frac{n_1}{p}+\frac{n_2}{q}=\frac{n_2-n_1}{R}$

I used the equation for the refraction on a spherical surface: $\frac{n_1}{p}+\frac{n_2}{q}=\frac{n_2-n_1}{R}$, where $n_1=1$ is the index of refraction of air, $n_2$ the index of refraction of the sphere, $R$ is the radius of the glass sphere, $p$ is the object distance which, since the rays are parallel I assumed to be infinite, $p=\infty$, and $q$ is the image distance, which should be $q=2R$. Substituting and solving for $n_2$ I get $n_2=2$.

Does my reasoning make sense? Thanks.

 

[TSny]

Looks good to me.

 

[SammyS]

Full size image.