No, that is not possible. If you take a root of a sum, can you say that this equals the sum of the roots of the terms? That's basically the same that you're asking!
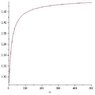
The above limit seems very nasty, but we can at least roughly estimate a bounding interval containing that limit value:
Note that, for fixed n, the MINIMUM value of the integrand is 1. Therefore, a lower bound for the integral equals 1, and the n'th root of 1, i.e, 1, is a lower bound for the whole expression.
Now, you may readily show that the maximum value for the integrand equals e^{\frac{n}{e}}, occurring at x=\frac{1}{e}.
Thus, an upper bound for the integral is e^{\frac{n}{e}}, and as an upper bound for the whole expression we have:
\sqrt[n]{e^{\frac{n}{e}}}=e^{\frac{1}{e}
Thus, our limit lies somewhere between 1 and e^{\frac{1}{e}}