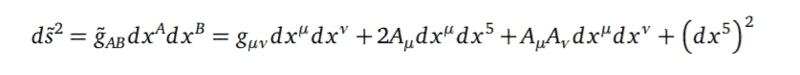Spinnor said:
Does string theory then have something like a line element that might in some proper limit look like the line element above.
You might like the 11d
Kaluza-Klein monopole solution to 11d supergravity. Its line element is of the form that you like to see, but for a spatially non-constant value of the dilaton.
Consider on a manifold of the form ##(\mathbb{R}^{0,1} \times \mathbb{R}^3 \times S^1) \times \mathbb{R}^6## the line element
$$
d s_{11}^2 =
- d t^2
+ (1+\mu/r) d s_{\mathbb{R}^3}^2
+ (1+ \mu/r)^{-1} (d x^{11} - A_i d x^i)^2
+ d s_{\mathbb{R}^6}^2
\,,
$$
where ##\mu## is some positive real constant (called the charge of the KK-monopole) and where ##r## denotes the distance in the ##\mathbb{R}^3##-factor from its origin. This means that the KK-circle is collapsed to zero size at the origin of the ##\mathbb{R}^3##-factor.
Here the factor ##\mathbb{R}^{0,1} \times \mathbb{R}^6## is the "worldvolume of the KK-monopole", which from the 10d perspective is the worldvolume of a D6-brane. If we think of this, in turn, as compactified (say wrapping a tiny Calabi-Yau) then the 5d part of the above geometry is
$$
d s_{5}^2 =
- d t^2
+ (1+\mu/r) d s_{\mathbb{R}^3}^2
+ (1+ \mu/r)^{-1} (d x^{11} - A_i d x^i)^2
\,,
$$
Far away from the locus of the monopole, hence for ##r \to \infty## this approaches
$$
- d t^2
+ d s_{\mathbb{R}^3}^2
+ (d x^{11} - A_i d x^i)^2
\,,
$$
which is the expression you were after in your first message (for flat spatial metric and with ##x^{11}## denoting what you denoted ##x^5##)