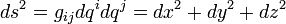What's wrong with the wiki link Mentz gave? Was it unclear? Too technical?
Basically, the Einstein convention is that you sum over repeated indices. In your example, ##g_{ij} dx^i dx^j## i and j are repeated, so you sum over i,j having all possible values. The Wiki link explains this - or tries to, so have several posters.
There is some ambiguity - what are all possible values? There are conventions for that too. But while textbooks will generally explain their conventions and follow them rigorously, you won't always see all posters here (including me) follow suit, leaving it up to the reader to sort out the minor ambiguities.
Wiki says:
In
general relativity, a common convention is that
- the Greek alphabet is used for space and time components, where indices take values 0,1,2,3 (frequently used letters are μ, ν, ...),
- the Latin alphabet is used for spatial components only, where indices take values 1,2,3 (frequently used letters are i, j, ...),
So using the above convention ##g_{ij} dx^i dx^j## in cartesian coordinates, where by modern convention ##t= x^0 \quad x = x^1 \quad y = x^2 \quad z=x^3## would be just dx^2 + dy^2 + dz^2, while ##g_{\mu\nu} dx^\mu dx^\nu## would be the space-time interval. Depending on more sign conventions, the space-time interval might be interpreted either as dx^2 + dy^2 + dz^2 - dt^2 , or possibly dt^2 - dx^2 - dy^2 - dz^2.
In cylindrical coordinates, we might have coordinates ##r, \phi, z## rather than x,y,z. If we identify ##x^1=r \quad x^2 = \phi \quad x^3=z## (the exact assignment here may vary even more between writers) then we would still write ##g_{ij} dx^i dx^j##, but this corresponds to ##dr^2 + r^2d\phi^2 + dz^2##, which you will hopefully recognize as the formula for the line element for distance in cylindrical coordinates. So in cylindrical coordinates with the given assignments ##g_{11}=1 \quad g_{22}=r^2 \quad g_{33}=1##. The result, though, gives you the distance in whatever coordinate system you use.
There are a lot of ambiguities in the notation, either a fuller explanation is given (in a well-written textbook), or the reader is expected to fill in the details from context.