bottle_shadow
- 2
- 0
- TL;DR
- Lack of understanding of the technique used to calculate the line integral.
Dear Physics Forums people,
My problem lies in understanding how the following line integral, which represents work done by the gravitational force, was calculated
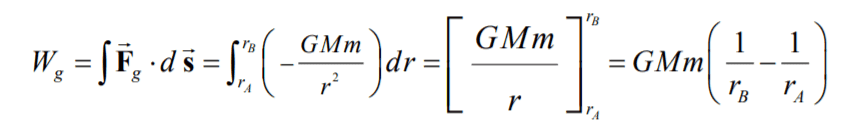
Specifically, in the integral after the 2nd = sign, they implicitly used \hat{r}\cdot d\vec{s} = dr
I wish to understand what is the argumentation for that.
Following is the picture that ought to provide the argumentation (but doesn't do it for me).
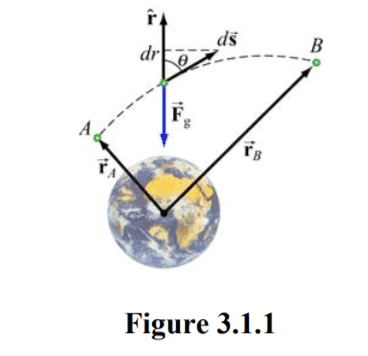
My problem lies in understanding how the following line integral, which represents work done by the gravitational force, was calculated
Specifically, in the integral after the 2nd = sign, they implicitly used \hat{r}\cdot d\vec{s} = dr
I wish to understand what is the argumentation for that.
Following is the picture that ought to provide the argumentation (but doesn't do it for me).