SUMMARY
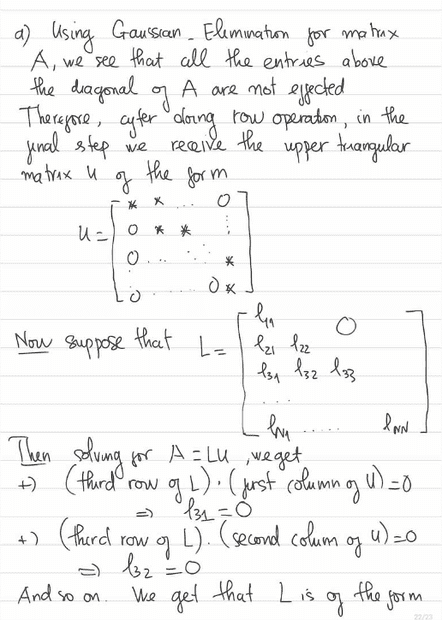
The discussion centers on LU Factorization, a method used in numerical analysis to decompose a matrix into a lower triangular matrix (L) and an upper triangular matrix (U). The user seeks feedback on their approach to LU Factorization, indicating a need for validation of their work. The conversation highlights the importance of understanding matrix decomposition techniques and their applications in solving linear equations.
PREREQUISITES
- Understanding of matrix operations and properties
- Familiarity with numerical analysis concepts
- Knowledge of linear algebra fundamentals
- Experience with computational tools for matrix manipulation
NEXT STEPS
- Study the algorithm for LU Factorization in detail
- Explore applications of LU Factorization in solving linear systems
- Learn about pivoting strategies in LU Factorization
- Investigate software tools like MATLAB or NumPy for implementing LU Factorization
USEFUL FOR
Students, educators, and professionals in mathematics, engineering, and computer science who are working with linear algebra and numerical methods will benefit from this discussion.