Linear First-Order Differential Equation

[DiamondV]

Hi,
so I am just starting to learn differential equations and we were told that you have to put the equation into

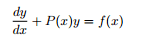this form.

In one of the examples in my lecture notes, which says
"Solve (x^2-9)dy/dx+xy=0, x>3" He then says we need to rearrange this into the form given above, so he does this by dividing across by x^2-9 and gets this.

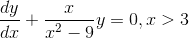
I understand that if you divide 0 by x^2-9 you get 0 but that still isn't a function of x

Now if you compare the form we put the equation into and the required form you will notice that

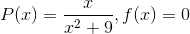
My issue is with the f(x). How is 0 a function of x? Arent we meant to have a function of x on the right as part of the required format?

 

[PeroK]

My issue is with the f(x). How is 0 a function of x? Arent we meant to have a function of x on the right as part of the required format?

If you are unhappy with $0$ just replace it with $x - x$, which perhaps you'll accept as a function of $x$.

 

[fresh_42]

$f(x) = λx$ is a function of $x$ for every $λ$, a straight through the origin. With $λ=0$ it just becomes the x-axis, but is still a straight through the origin and a function of $x$. Also $f(x) =$any constant is a function of $x$.

 

[HallsofIvy]

My issue is with the f(x). How is 0 a function of x? Arent we meant to have a function of x on the right as part of the required format?

A constant function, f(x)= any number is also a function! The basic definition of "function" is "a set of ordered pairs such that no two pairs have the same first value". The function f(x)= 0 for all x is the set of ordered pairs {(x, 0)} where x can be any number.