Linear force of a syringe pump plunger

[kaadeeka]

Hi all,

I am looking for the correct calculation of the torque (or linear force) that is needed on a syringe plunger to overcome a backpressure at the nozzle of 20,000 psi.

I have to decide which syringe pump I will be using for my application, but their is a lot of choice and mainly I need enough linear force to overcome 20,000 psi back pressure.

The plunger has a diameter of 0.4 inch , the nozzle has an internal diameter of 0.02 inch. Let us say that the syrine is filled with water and the backpressure is also coming from water that is restricted by a back pressure regulator of 20,000 psi (not the real case, but to keep it simple).

In attachment I have put a drawing of my question.

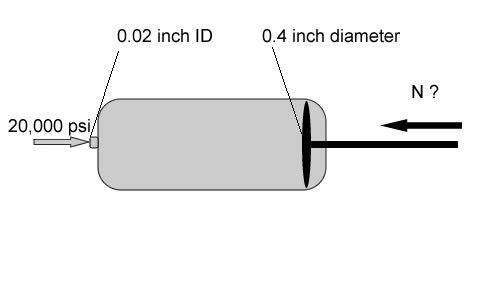
I hope someone can help. Apparently this is not such an easy question, as all syringe pump manufacturers give me an ambiguous answer.

 

[Simon Bridge]

You have 20000PSI at the hole ... if the plunger didn't move, what would be the pressure inside the syringe?

 

[Baluncore]

20,000 psi is quite a high pressure. Most hydraulic systems operate below 3,000 psi.
Water jet cutting and some common rail diesel injection systems use 20,000 psi.
Those pressures are very dangerous because a pinhole leak in a fitting can amputate a finger before you realize what is happening.

The answer to your question will come out at a little over a one ton force.
Take care.

 

[kaadeeka]

You have 20000PSI at the hole ... if the plunger didn't move, what would be the pressure inside the syringe?

Pressure would be atmospheric, because the pressure is building up the moment the syringe starts flowing. The syringe has to be able to flow so fast that the whole system reaches a backpressure of 20,000 psi.

I don't know if you are familiar with HPLC, but this is exactly what I am planning to do with the syringe pump.

It means that the syringe pump will be connected to a 'column' filled with small particles of 2 μm. This will give a high back pressure if the flow is coming close to 1 ml/min. The syringe pump has to be able to go as high as 20,000 psi.

 

[kaadeeka]

20,000 psi is quite a high pressure. Most hydraulic systems operate below 3,000 psi.
Water jet cutting and some common rail diesel injection systems use 20,000 psi.
Those pressures are very dangerous because a pinhole leak in a fitting can amputate a finger before you realize what is happening.

The answer to your question will come out at a little over a one ton force.
Take care.

What all respect, but I don't think this is right...

 

[Baluncore]

The pressure you specify is in psi, that is, pounds per square inch. No matter what the section of the vessel or tube is, the pressure will be 20,000 psi.

If the pressure connected to the one side of the piston is 20,000 psi and the other side is atmospheric then the force on the piston will be 20,000 multiplied by the area of the piston.

Diameter = 0.4” therefore radius = 0.2”
Area = Pi * r * r = 0.126 square inches.
Force = 0.126 * 20,000 = 2515. pounds force.
2515 pounds force = 2515 / 2.2046 kg force = 1140 kg force = 1.14 tonne force.
1140 kg force = 1140 * 9.807 Newton = 11180 N.

 

[kaadeeka]

yep, I just figured it out myself. I was confused with the term 'ton', which sounded as 'really really a lot', but is actually just 1000 kg ... :-)