trojsi
- 17
- 0
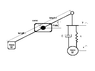
From this mechanical part (attached), I need to derive a differential equation relating mass 'x' position to hinge 'y' position.
\ddot{x}m + b\dot{x} + cx = F
The link l would be rotating. I am confused about considering the displacement of x with reference to y. Would this change the differential equation by replacing x with (x-y) ?
I derived an equation to relate 'y' with \theta ;
y = lsin(\theta)
Finally I also need to derive a differential equation from the previous two to relate the loading torque on the shaft for some rotation theta.
\tau = (\ddot{x}m + b\dot{x} + cx)lcos(\theta)
I would really appreciate if you can give me some hints on my work. thanks
\ddot{x}m + b\dot{x} + cx = F
The link l would be rotating. I am confused about considering the displacement of x with reference to y. Would this change the differential equation by replacing x with (x-y) ?
I derived an equation to relate 'y' with \theta ;
y = lsin(\theta)
Finally I also need to derive a differential equation from the previous two to relate the loading torque on the shaft for some rotation theta.
\tau = (\ddot{x}m + b\dot{x} + cx)lcos(\theta)
I would really appreciate if you can give me some hints on my work. thanks
Attachments
Last edited: