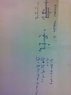Load on a beam: More unknowns than equations?

Click For Summary
The discussion centers on analyzing a propped cantilever beam, which is identified as statically indeterminate. The user struggles to determine the reaction forces necessary for their analysis. It is suggested that additional equations are needed, particularly using the conditions of zero deflection at point B and zero deflection and slope at point A. The presence of a hinge between points A and B indicates that the bending moment at the hinge is zero, providing an essential equation for solving the problem. Understanding these principles is crucial for accurately analyzing the load on the beam.
Marvin94
Messages
41
Reaction score
0

Homework Statement



IMG_20150802_193659.jpg


Homework Equations


FBD and all forces and moments = 0

The Attempt at a Solution


Sketched in the image.

So, I don't know how to go on with my analysis of the load, since I can't determine the reaction forces. Can someone please help me? Thanks in advance!
 

Attachments

  • IMG_20150802_193659.jpg
    IMG_20150802_193659.jpg
    23.6 KB · Views: 512
Physics news on Phys.org
This beam is what is known as a "propped cantilever". It is statically indeterminate.

You will have to write additional equations, knowing that the deflection = 0 at B and the deflection and slope of the beam at A are both equal to zero.
 
There seems to be a hinge between A and B. This makes it statically determinate. At the hinge, the bending moment would be zero, and this gives you the additional equation you need to solve the problem.
 

Similar threads

Statics engineering: Beam bending problem
  • · Replies 8 ·
Replies
8
Views
2K
Engineering Statics, Finding Reaction forces for A and H
  • · Replies 6 ·
Replies
6
Views
2K
Engineering Loads on a shaft with V-Belts
  • · Replies 2 ·
Replies
2
Views
3K
Finding Unknown Forces on a Beam Structure
  • · Replies 3 ·
Replies
3
Views
2K
Calculate Axial Load on Column from Beam Transfer
  • · Replies 4 ·
Replies
4
Views
3K
Solve Castigiliano Method for Continuous Beam Problem
  • · Replies 8 ·
Replies
8
Views
2K
Calculating Beam Load for One Way Slab: Analysis and Solutions
  • · Replies 1 ·
Replies
1
Views
2K
A beam: need to calculate its max moment and deflection
  • · Replies 1 ·
Replies
1
Views
2K
Beam with two supports + spring
  • · Replies 1 ·
Replies
1
Views
3K
Solving AB Beam Reactions with Hyperstatic System
  • · Replies 1 ·
Replies
1
Views
2K