SUMMARY
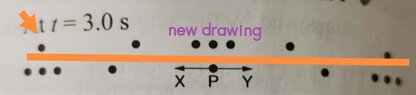
When analyzing the position of particles in a sound wave after 1.5 periods, it is established that every compression transforms into a rarefaction and vice versa. The discussion clarifies that at t=0, particles P1, P2, and P3 create a compression, while P4, P5, and P6 form a rarefaction, and P7, P8, and P9 create another compression. At t=3 seconds, the configuration changes, with P2 and P3 contributing to a rarefaction, while P4, P5, and P6 remain a compression, and P7 and P8 form part of another rarefaction. The omission of particles P1 and P9 in the diagram is attributed to space constraints rather than an error in representation.
PREREQUISITES
- Understanding of sound wave mechanics
- Familiarity with wave properties such as compression and rarefaction
- Basic knowledge of particle representation in wave diagrams
- Ability to interpret graphical representations of wave behavior
NEXT STEPS
- Study the principles of wave propagation in different mediums
- Learn about the mathematical representation of sound waves
- Explore the concept of wave interference and its effects on sound
- Investigate the impact of particle density on wave speed and behavior
USEFUL FOR
Students of physics, educators teaching wave mechanics, and anyone interested in the dynamics of sound waves and their graphical representations.