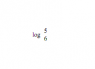maplesyrup23
- 10
- 0
Hi Physics Forums,
I understand that I usually need to show that I've attempted a question in order to get feedback, but I have absolutely no idea how to approach this one Calculus Log question.
Base = 10
log (2) = 0.301103, log (3) = 0.47715
a.) Find log base 6 (5)
b.) Estimate the number of digits in 15^10
I'd appreciate being pointed in the right direction.
I understand that I usually need to show that I've attempted a question in order to get feedback, but I have absolutely no idea how to approach this one Calculus Log question.
Base = 10
log (2) = 0.301103, log (3) = 0.47715
a.) Find log base 6 (5)
b.) Estimate the number of digits in 15^10
I'd appreciate being pointed in the right direction.