SUMMARY
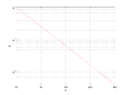
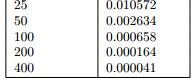
The discussion focuses on the interpretation of log-log graphs, specifically the relationship between variables $N$ and $E$. It establishes that a log-log plot can represent power relationships of the form $y=a x^b$, allowing for the determination of coefficients $a$ and $c$. The participants confirm that the linear representation of $\log E$ against $\log N$ leads to the equations $\log E = a \log N + c$ and $E = 10^c N^a$. The calculations provided by a user yield $a = -2$ and $c = \log(656) - 2$, although discrepancies with Wolfram|Alpha's results raise questions about accuracy.
PREREQUISITES
- Understanding of logarithmic functions and properties
- Familiarity with power laws and their graphical representations
- Knowledge of least-squares fitting techniques
- Basic proficiency in using mathematical software like Wolfram|Alpha
NEXT STEPS
- Study the principles of log-log graph analysis in detail
- Learn about least-squares fitting methods for data approximation
- Explore the implications of significant figures in mathematical calculations
- Investigate the use of logarithmic transformations in data analysis
USEFUL FOR
Mathematicians, data analysts, and researchers interested in power law relationships and log-log graph interpretations will benefit from this discussion.