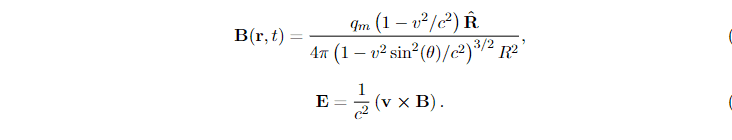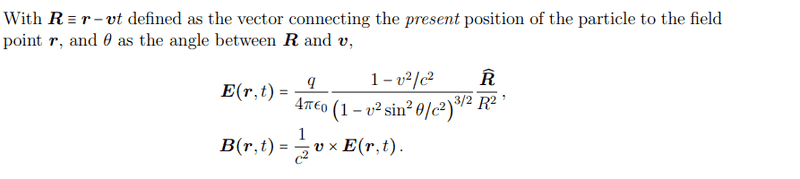I don't think you took into account the negative sign in the relation ##\mathbf{B} \rightarrow -\mu_0 \epsilon_0 \mathbf{E}_m##.
Also, I'm guessing that you've somehow introduced the volume of the charge, ##\tau##, with the intention of replacing ##\rho \tau## by ##q##.
However, it's not so simple. For example, the potentials ##V## and ##\mathbf{A}## depend on the sources ##\rho## and ##\mathbf{J}## at
retarded times ##t_r##. This is discussed in Griffiths (pages 430 - 431 in the 3rd edition) or see
section 21-5 of the Feynman Lectures. As shown there, it turns out that ##\int \rho(\mathbf{r'}, t_r) d\tau' \neq q##.
But,
we don't need to worry about this because exactly the same subtleties occur for the magnetic monopole. The transcription ##\rho \rightarrow \mu_0 \epsilon_0 \rho_m## means that ##q## will get replaced by ##\mu_0 \epsilon_0 q_m## in the final equations.
So, the formula for the electric field of a moving electric charge is given to be $$\mathbf{E}(r, t) = \frac{q}{4 \pi \epsilon_0}\frac{1-v^2/c^2}{\left(1-v^2 \sin^2 \theta /c^2 \right)^{3/2}}\frac{\hat{\mathbf{R}}}{R^2}$$ It should now be easy to translate this to the expression for ##\mathbf{B}_m(r, t)## for the magnetic monopole.
Likewise, you can translate ##\mathbf{B}(\mathbf{r}, t) = \frac 1 {c^2} \mathbf{v} \times \mathbf{E}(\mathbf{r},t)## to get ##\mathbf{E}_m(\mathbf{r},t)##.