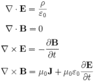Magnetic Field of a Moving Charge and the Displacement Current

[tade]

We all know a moving charge generates a magnetic field.

A moving charge also generates a displacement current ∂E/∂t.

Is the magnetic field generated entirely due to the presence of the displacement current, or is there an independent, separate effect which contributes to the magnetic field?

 

[anorlunda]

Here are Maxwell's Equations. Do you find your answer there?

 

[tade]

Here are Maxwell's Equations. Do you find your answer there?

View attachment 239953

ok, so, looking at the last Maxwell equation, I'm unclear about the distinction between the physical J-current and the displacement current in generating the magnetic field of a moving charge.

I was wondering if all magnetic fields due to J currents are just due to displacement currents caused by and associated with moving charges.

Wondering if attributing B-fields to J-currents was just a simpler way of expressing the effects of displacement currents associated with moving charged particles. With the addition of an additional term of displacement currents in empty space which are not directly associated with moving charges.

 

[anorlunda]

I was wondering if all magnetic fields due to J currents are just due to displacement currents caused by and associated with moving charges.

I think that last equation clearly shows that it is the sum of the two.

 

[tade]

I think that last equation clearly shows that it is the sum of the two.

Yeah, to elaborate on #3, I was wondering if attributing B-fields to J-currents was just a simpler way of expressing the effects of displacement currents associated with moving charged particles. With the addition of an additional term of displacement currents in empty space which are not directly associated with moving charges.

Considering the sum of the two, should we add a displacement current correction to the equation in the yellow box?

 

[anorlunda]

Considering the sum of the two, should we add a displacement current correction to the equation in the yellow box?

If you do, you arrive at Ampere's Law, which is the 4th Maxwell Equation. The second terms is called Maxwell's correction to Ampere's Law.

You're going in circles.

 

[tade]

If you do, you arrive at Ampere's Law, which is the 4th Maxwell Equation. The second terms is called Maxwell's correction to Ampere's Law.

You're going in circles.

Apologies if I sound terse, no intention to, though it might appear that way in text.

Back to the question, sorry, what I meant was, I'd like to learn more about Maxwell's correction to the magnetic field of a single moving charged particle.

 

[anorlunda]

I don't know how much math you have in your background.

This article isn't the easiest
https://en.wikipedia.org/wiki/Displacement_current

 

[ZapperZ]

Apologies if I sound terse, no intention to, though it might appear that way in text.

Back to the question, sorry, what I meant was, I'd like to learn more about Maxwell's correction to the magnetic field of a single moving charged particle.

I don't quite understand the issue here. The displacement current is just the rate of change in the E-field. It is not the real current. I thought that it is clear from that equation, and from the origin of this term via the application of Ampere's circuital law?

{scratching head}

Zz.

 

[tade]

I don't quite understand the issue here. The displacement current is just the rate of change in the E-field. It is not the real current. I thought that it is clear from that equation, and from the origin of this term via the application of Ampere's circuital law?

{scratching head}

Zz.

yeah, but it probably contributes to the magnetic field of a moving charge right?

 

[anorlunda]

yeah, but it probably contributes to the magnetic field of a moving charge right?

Wrong.

It is time for you to realize that you have some kind of misconception.

 

[tade]

Wrong.

It is time for you to realize that you have some kind of misconception.

Sorry, could you elaborate?

Lol, "It is time", but we haven't started for long

 

[bhobba]

Sorry, could you elaborate?

Where do Maxwell's Equations come from? See:
http://www.cse.secs.oakland.edu/haskell/Special Relativity and Maxwells Equations.pdf

Its all just basically a relativistic effect.

Thanks
Bill

 

[tade]

Where do Maxwell's Equations come from? See:
http://www.cse.secs.oakland.edu/haskell/Special Relativity and Maxwells Equations.pdf

Its all just basically a relativistic effect.

Thanks
Bill

Sorry, but I'm just trying to figure out the relationships between the J and displacement currents with regards to the magnetic field of a single moving charged particle.

 

[PeroK]

I was wondering if all magnetic fields due to J currents are just due to displacement currents caused by and associated with moving charges.

Wondering if attributing B-fields to J-currents was just a simpler way of expressing the effects of displacement currents associated with moving charged particles. With the addition of an additional term of displacement currents in empty space which are not directly associated with moving charges.

In general, you can have a current and a magnetic field without an electric field. If a steady current is flowing in a neutral wire then there is no electric field. The magnetic field is due entirely to the current. This is the "magnetostatics" case.

Note also that in many cases the displacement current is very small, which is why it was not discovered experimentally.

 

[tade]

In general, you can have a current and a magnetic field without an electric field. If a steady current is flowing in a neutral wire then there is no electric field. The magnetic field is due entirely to the current. This is the "magnetostatics" case.

Note also that in many cases the displacement current is very small, which is why it was not discovered experimentally.

ok, so does that means that there's a tiny correction to the B-field of a moving charge due to the displacement current?

 

[PeroK]

ok, so does that means that there's a tiny correction to the B-field of a moving charge due to the displacement current?

If you want to calculate the B-field, you need to take into account both the current and the changing E-field. Both are directly caused by the moving charge. It's not like the displacement current is something physically separate.

 

[bhobba]

If you want to calculate the B-field, you need to take into account both the current and the changing E-field. Both are directly caused by the moving charge. It's not like the displacement current is something physically separate.

Exactly. They are both simply a relativistic effect. There is no relationship other than they are 'caused' by the same thing - relativity - but are two different processes.

To the OP the link I gave did not explain relativity the way I would which the following does:
http://www2.physics.umd.edu/~yakovenk/teaching/Lorentz.pdf

We see there is an undetermined constant in the derivation, c (it of course turns out to be the speed of light - but that is an experimental matter) - and logically could be infinity which would lead to the standard Galilean Transformations. Now apply this, with the undetermined c to Coulombs Law and low and behold, as the paper shows, you get Maxwell's equations - still with an undetermined c. But a little experimentation with currents soon shows magnetic fields exist and that constant is the speed of light. That is proof of both moving charges having magnetic fields and the constant c being finite. Physically its due to the length contraction of the current increasing it's density in another frame - a relativistic effect. That a changing electric field generates a magnetic is also a relativistic effect this time caused by the fact the field tensor Fuv can be written in the standard form using the four potential Au ie Fuv = ∂uAv - ∂vAu. Immediately this implies ∂u∂vFuv =0 so defining ∂uFuv = Jv as the four current we see immediately whatever it is, is conserved. Write out the definition of the 4 current and you get the displacement current. The root cause is the same - relativity - but applied to two different things - charge continuity from the definition of the 4 current, and charge contraction. There is no link other than that.

Understanding Maxwell's equations is an interesting exercise. I gave one explanation based on Coulombs Law and Relativity. It was at a good level of rigor. But if you relax that requirement a bit then the following will likely be found interesting:
https://arxiv.org/abs/1507.06393

An excellent exercise is going through the paper and finding just what assumptions it makes. One is obvious - it assumes Fαβ is a field, but its explanation is highly dubious at best - actually its downright wrong. If you want to discuss the paper further best to start another thread.

Thanks
Bill

 

[tade]

If you want to calculate the B-field, you need to take into account both the current and the changing E-field. Both are directly caused by the moving charge. It's not like the displacement current is something physically separate.

sorry, I meant a tiny correction to the formula in the yellow box, I'm guessing yes?

 

[PeroK]

sorry, I meant a tiny correction to the formula in the yellow box, I'm guessing yes?

I would say the equation in the yellow box is simply wrong. The Biot-Savart law applies to steady currents, and a single moving charge is not a steady current.

But, perhaps, some texts tend to gloss over this?

 

[tade]

I would say the equation in the yellow box is simply wrong. The Biot-Savart law applies to steady currents, and a single moving charge is not a steady current.

But, perhaps, some texts tend to gloss over this?

I think almost every introductory textbook uses that equation.

 

[hutchphd]

I think almost every introductory textbook uses that equation.

May I suggest to all Feynman's Lectures II-26: " Lorentz Transformations of the Fields".

http://www.feynmanlectures.caltech.edu/II_26.html

I believe he speaks directly to this question and I will not presume to summarize.

 

[bhobba]

I think almost every introductory textbook uses that equation.

Unfortunately introductory textbooks in physics do leave some issues either not explained, or actually wrong and corrected later. Its a while since I read introductory EM textbooks so I can't comment (my first was from Wiley and is now falling to pieces). Feynman is usually reliable, but as just about everyone notes is not the best actual textbook - but just about always recommended as supplementary reading. It is the book for those not necessarily interested in doing well on tests, but in understanding physics.

Later you will likely study Jackson, but I humbly recommend of course Feynman (which is available free, but I purchased the books myself) and Schwinger's book:
https://www.amazon.com/dp/0738200565/?tag=pfamazon01-20

IMHO Schwinger is better than Jackson, and I would get a copy purely for reference. It is always my go-to book on EM. Don't worry that its graduate level and you quite likely are not. That's the purpose of reference books - they become your go-to book not just for refreshing your knowledge of things, but at first while you do not get their full impact - you understand it - but its full value comes later after a number or readings over many years. For Classical Mechanics Goldstein in usually recommended for that like Jackson for EM - but IMHO Landau - Mechanics leaves Goldstein for dead. Landau - Classical Theory Of Fields is also excellent - but IMHO Schwinger is better - which is saying something since I practically worship Landau. Schwinger seems to combine the best of Jackson and Landau (the issue with Landau is he is quite terse).

Thanks
Bill

 

[hutchphd]

I agree with you, but it is like a morning stroll to read Feynman. And I always learn something

Feynman is usually reliable

For the record I will presume to summarize to the extent that he does derive the "Biot-Savart" result for a point charge rigorously in the non-retarded time limit by transforming the fields.

 

[bhobba]

I agree with you, but it is like a morning stroll to read Feynman. And I always learn something.

Feynman is like that, as well as Landau. Which is why I got both for reference purposes. Schwinger is like that in spades. Its just that personally I mined EM to my satisfaction ages ago.

Thanks
Bill

 

[hutchphd]

Schwinger is like that in spades.

I need to get a copy and look at it again...never had it for a course. I did teach an undergrad course using Griffiths and found it very good as a textbook.
And Jackson is, well, Jackson...not my favorite but not really replaceable either.

 

[tade]

@bhobba @hutchphd @PeroK thanks guys, I was checking out Jefimenko's equations, and they obscure the symmetry between the E and B fields.
There are no magnetic monopoles or magnetic currents.

But even without magnetic monopoles, the symmetry can be clearly seen in Maxwell's equations.

So, do you know of any formulas for the E and B fields which both use retarded time and show the symmetry between them?