Magnetic Field of Rectangular Loop: Solving for P Far Away

[stunner5000pt]

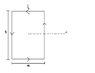
CXosnider a rectangular loop carrying a current i as shown in teh figure. Point P is located a distance x from the cneter of the loop. Find an epxression for tha mgnetic field at P due to the current loop assuming that P is very far away.
WIth \mu = iA = iab obtain an expression similar to that of a circular looop which is B = \frac{\mu_{0} \mu}{2 \pi x^3}
for the field due to a distant dipole at points in the plane of the loop (perpendicular to the axis.)
Hint: Opposite sides can we treated together but consider carefully the direction of B due to each side

Well
for vertical sides (sides of length b) the magnetic field due to them both is zero because of the right rule, their magnetic field are in opposite directions and equal (equal becuase x >> a/2)

for the hirzontal sides however, the same doesn't not apply, the magnetic field is not zero since due to them both th magnetic field points out of the page.

not since x is big am i right in assuming taht \sqrt{x^2 + \frac{b^2}{4}} \approx x ??
in that case
B = \frac{2 \mu_{0} i}{2 \pi x} = \frac{\mu_{0} i}{\pi x}
is this right?

im not sure ho to proced with teh second part of the quesiton..

 

[Tide]

The contributions from the vertical sides don't exactly cancel and for the horizontal sides you left out a geometric factor (vector cross product in Biot-Savart).

 

[stunner5000pt]

i understnad taht that is true... but can't i do the approximation ??

for the vertical pieces of wire ..
well for 2 pieces of wire
B = 2 \frac{\mu_{0} i}{4 \pi} \int \frac{ds \times x}{x^3}
here s is constant and r is constant

B = 2 \frac{\mu_{0} i b}{4 \pi x^2} is that correct?

 

[Tide]

You can do an approximation but just not the one you're attempting!

Biot-Savart will involve integrals over the length of each side of quantities like

\frac {d\vec l \times \vec r}{r^2}

E.g., the right side is a/2 units from the center so that \vec r = (x-a/2)\hat i + y \hat j where y is the vertical coordinate (the variable you will integrate over). Also, d\vec l = dy \hat j so you can form the vector cross product d\vec l \times \vec r. You'll integrate this (vector) from y = -b/2 to +b/2. Notice that r^2 = (x-a/2)^2 + y^2

Similarly, for the left side \vec r = (x+a/2)\hat i + y \hat j. In this case, r^2 = (x + a/2)^2 + y^2. The two integrals (from left side and right side) do not cancel out.