Magnetic force on a current carrying wire

[Biker]

I was wondering what would happen if you have a current carrying wire that makes an angle with the magnetic field and how to describe its motion. Prepare yourself for the bad drawing.

I will first show how the method I used works for a simpler case where Magnetic field and current are perpendicular: https://i.imgur.com/c8HYxzt.png
Assume a charge $Q$ it will experience magnetic force to the right which will give it a speed $V$ to the right (as the whole wire moves). This creates another magnetic force pointing downward which is the reason for the back emf, This also conserves energy.

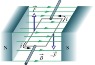
Now for this case: https://i.imgur.com/hWsaJAI.png
There will be a force $F_{m1}$ into the page and a velocity $V_1$ into the page will result from it which will create the force $F_{m2}$ as in the picture That will have a component in the x and y direction, I will ignore the x direction assuming we can keep a steady current, This will create a velocity $v_2$ in the x direction which finally creates $F_{m3}$ out of the page, Now this conserves energy too and it shows that the wire will move in x direction and into the page. You can link the movement in those directions together to get a function of distance

Is this approach correct? Any simpler ways?

 

[kuruman]

For purposes of calculating the velocity of the wire, you cannot just consider a wire segment because that segment is attached to another and another and so on to form a closed loop. Without a closed loop you don't have a current. So you have to consider the velocity of the entire loop. Now it turns out that a current loop in a uniform magnetic field experiences no net force, therefore to get a force that will accelerate the loop you will need a non uniform magnetic field. Nevertheless, the local force on a wire segment carrying current $I$ no matter what the angle of the wire with respect to the field, is given by the well known relation $\vec F = I \vec L \times \vec B$ where $\vec L$ has magnitude equal to the segment length and is directed along the current. The cross product takes care of the angle.

 

[Biker]

For purposes of calculating the velocity of the wire, you cannot just consider a wire segment because that segment is attached to another and another and so on to form a closed loop. Without a closed loop you don't have a current. So you have to consider the velocity of the entire loop. Now it turns out that a current loop in a uniform magnetic field experiences no net force, therefore to get a force that will accelerate the loop you will need a non uniform magnetic field. Nevertheless, the local force on a wire segment carrying current $I$ no matter what the angle of the wire with respect to the field, is given by the well known relation $\vec F = I \vec L \times \vec B$ where $\vec L$ has magnitude equal to the segment length and is directed along the current. The cross product takes care of the angle.

I was considering placing this conductor only in the magnetic field and the rest of the loop outside it. I just wanted to know what would happen.

Also, yes the force is ILxB but this force causes the wire to move in a certain direction which gives the charges a velocity in that direction so another magnetic force will appear that was the basis of what I have done

 

[kuruman]

I was considering placing this conductor only in the magnetic field and the rest of the loop outside it. I just wanted to know what would happen.

I see. What would happen in the general case is that the loop will experience a net force (it's in a non-uniform field) the direction of which will depend on the cross product. This force will either push it away or toward the field region. In addition, the force will generate a torque that will make the loop rotate about its center of mass. Even if one ignores the back emf, writing out and solving the equations of motion is a messy job because one has to figure out how both the magnitude and direction of $\vec L$ in $I\vec L \times \vec B$ change as the loop moves.

 

[Biker]

I see. What would happen in the general case is that the loop will experience a net force (it's in a non-uniform field) the direction of which will depend on the cross product. This force will either push it away or toward the field region. In addition, the force will generate a torque that will make the loop rotate about its center of mass. Even if one ignores the back emf, writing out and solving the equations of motion is a messy job because one has to figure out how both the magnitude and direction of $\vec L$ in $I\vec L \times \vec B$ change as the loop moves.

Ah, so if we consider the hole loop (Rigid object?) the initial force will be into the page which will result in the center of mass moving into and that the loop will rotate in 3d? But this will add a component of velocity to the charges velocity's which we should take this into account too and consider the magnetic force result from that..?

So The FBD I gave above is correct? and yes I had to make some assumptions to simplify the calculations about L and B. A complicated motion it will be.

I was thinking at the beginning of the wire being able to move freely in the field without the loop by having the loop fixed and giving the loop some length so the wire can move but not very realistic :(

 

[kuruman]

Ah, so if we consider the hole loop (Rigid object?) the initial force will be into the page which will result in the center of mass moving into and that the loop will rotate in 3d?

Yes.

I was thinking at the beginning of the wire being able to move freely in the field without the loop by having the loop fixed and giving the loop some length so the wire can move but not very realistic :(

Don't give up so fast. You can have a non-rigid loop. Suppose you clamp down a U-shaped piece of wire connected to a battery. At the two ends of the U you electrically connect a rigid straight piece of wire using flexible wire. Then you can suspend the wire segment in the field and let it go where it will. Of course, in any FBD you draw for this you ave to include the tensions from the connecting wires. Those are also missing from the original FBD you posted. Still, the motion will be complicated.

 

[Biker]

Yes.

Don't give up so fast. You can have a non-rigid loop. Suppose you clamp down a U-shaped piece of wire connected to a battery. At the two ends of the U you electrically connect a rigid straight piece of wire using flexible wire. Then you can suspend the wire segment in the field and let it go where it will. Of course, in any FBD you draw for this you ave to include the tensions from the connecting wires. Those are also missing from the original FBD you posted. Still, the motion will be complicated.

Just a follow up question, Sorry.

In the case of a current loop (rectangular for simplicity) in a magnetic field (Motor), Calculating the torque at any moment will also be difficult if the magnetic field not perpendicular to the axis of rotation? Since the same complicated motion will happen here, Where components of the velocity as the loop rotates will affect the torque.

Is this correct?

 

[kuruman]

A rectangular loop in a motor is simpler in that its motion repeats after one revolution and the net force on it is zero because the loop is constrained to move about its axis. What counts for the induced emf is the component of the B-field perpendicular to the plane of the motor so you need to find that as a function of angle. Remember that the perpendicular component is $B_{\perp}=\vec B \cdot \hat n$ where $\hat n$ is the unit vector normal to the plane of the loop. The torque is $\vec{\tau}=IA\vec B \times \hat{n}$ where $I$ is the current and $A$ is the area of the loop. Thus, if you can find $\hat n(t)$, you can write equations for the induced emf and the torque on the loop.

 

[Biker]

A rectangular loop in a motor is simpler in that its motion repeats after one revolution and the net force on it is zero because the loop is constrained to move about its axis. What counts for the induced emf is the component of the B-field perpendicular to the plane of the motor so you need to find that as a function of angle. Remember that the perpendicular component is $B_{\perp}=\vec B \cdot \hat n$ where $\hat n$ is the unit vector normal to the plane of the loop. The torque is $\vec{\tau}=IA\vec B \times \hat{n}$ where $I$ is the current and $A$ is the area of the loop. Thus, if you can find $\hat n(t)$, you can write equations for the induced emf and the torque on the loop.

I can only prove these equation only if I have a magnetic field pointing to the right in a horizontal plane.

How do you prove that generally? How do you prove it for any arbitrary shape? I haven't taken linear algebra but I know a bit about it and planning to study it soon.

Thanks in advance.

 

[kuruman]

I can only prove these equation only if I have a magnetic field pointing to the right in a horizontal plane.

OK, so you have a magnetic field in the x-direction. What else do you have? Can you post a picture?

How do you prove that generally? How do you prove it for any arbitrary shape?

Prove what generally? What is it that has arbitrary shape? If the shape of whatever is too arbitrary one may not be able to describe it mathematically.

I haven't taken linear algebra but I know a bit about it and planning to study it soon.

You don't need linear algebra for this, but you do need to understand vectors.

 

[Biker]

OK, so you have a magnetic field in the x-direction. What else do you have? Can you post a picture?

Prove what generally? What is it that has arbitrary shape? If the shape of whatever is too arbitrary one may not be able to describe it mathematically.

You don't need linear algebra for this, but you do need to understand vectors.

I mean this, I can prove the equation you gave above for this condition where you have a rectangular loop rotating and the magnetic field is pointing as in the picture. I also read that the equation for rectangular loop will work for any arbitrary loop which I kinda can see why if the magnetic field points in the same direction.

However what I can't do is describe if the magnetic fields makes an angle or not in the same as the diagram and I can't describe what would happen for an arbitrary shape loop with a magnetic field that makes an angle. I can't find a logical way to evaluate the integral except in the direction as that in the picture.

 

[kuruman]

In the picture you posted the loop has a magnetic moment $\vec m = IA \hat n$ where $\hat n$ is always perpendicular to the loop and at the instant shown points straight up. Also, at this instant the torque on the loop has magnitude $\tau = IAB$ and points into the screen, sort of. Call the torque direction y, call the direction of the field x and the direction straight up z. As the loop rotates, the magnetic moment rotates in the zx plane perpendicular to the y-axis. If at the instant shown in the figure we take t = 0, then the normal to the loop at subsequent times can be written as $\hat{n}(t)=\sin(\omega t)\hat x+\cos(\omega t)\hat z$. The field is fixed and is given by $\vec B = B \hat x.$ With these expressions you can find the torque and the induced emf at any time t. It doesn't matter if the loop is irregular; it still has a magnetic moment $\vec m = IA \hat n$.

Does this answer your question?

 

[Biker]

In the picture you posted the loop has a magnetic moment $\vec m = IA \hat n$ where $\hat n$ is always perpendicular to the loop and at the instant shown points straight up. Also, at this instant the torque on the loop has magnitude $\tau = IAB$ and points into the screen, sort of. Call the torque direction y, call the direction of the field x and the direction straight up z. As the loop rotates, the magnetic moment rotates in the zx plane perpendicular to the y-axis. If at the instant shown in the figure we take t = 0, then the normal to the loop at subsequent times can be written as $\hat{n}(t)=\sin(\omega t)\hat x+\cos(\omega t)\hat z$. The field is fixed and is given by $\vec B = B \hat x.$ With these expressions you can find the torque and the induced emf at any time t. It doesn't matter if the loop is irregular; it still has a magnetic moment $\vec m = IA \hat n$.

Does this answer your question?

Sorry I wasn't clear, I already done that for this case. I was asking for this:
My question is why it doesn't matter if it is irregular? Does it only not matter when the B in the x direction only or no? How can we prove that it doesn't?

Also, What if B has components in x and z direction? How would that change the calculation? Doesn't it cause the complex diagram that I showed in the first of the thread?

 

[kuruman]

My question is why it doesn't matter if it is irregular?

Say your rotating loop is irregular. It still has an area $A$ and a current $I$ and a magnetic moment $\vec m = IA \hat n (t)$. If the field is tilted relative to the axis of rotation and has a y-component then you have to write it as $\vec B = B_x\hat x+B_y \hat y$, but the torque is still $\vec{\tau}=\vec m \times \vec B$ and the magnetic flux is still $\Phi=\vec B \cdot \hat{n}(t)$. Just take the appropriate cross and dot products of whatever vectors you have. The torque and flux equations are general in that regard.

 

[Biker]

Say your rotating loop is irregular. It still has an area $A$ and a current $I$ and a magnetic moment $\vec m = IA \hat n (t)$. If the field is tilted relative to the axis of rotation and has a y-component then you have to write it as $\vec B = B_x\hat x+B_y \hat y$, but the torque is still $\vec{\tau}=\vec m \times \vec B$ and the magnetic flux is still $\Phi=\vec B \cdot \hat{n}(t)$. Just take the appropriate cross and dot products of whatever vectors you have. The torque and flux equations are general in that regard.

And all planar shapes have the same magnetic moment expression because?
Sorry again. Should have put the questions together.

 

[kuruman]

And all planar shapes have the same magnetic moment expression because?

http://julian.tau.ac.il/bqs/em/magmoment.pdf