Magnetic induction in toroidal transformers

[Jdo300]

Hello,

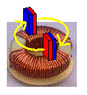
If I take a small toroidal transformer and rotate a magnet over the top of it with the magnet's poles at 90 degrees to the coils, how does the presence of the permiable core affect the Lenz forces that are exerted on the magnet? Would the lenz forces be very small since the magnetic field of the coils are drawn inside the core or am I missing something here? I drew up a simple illustration to show what I mean. Also, how does one calculate the amount of current induced in the coils with the magnet(s) in this configuration?

Thank you,
Jason O

 

[Danger]

Hi, Jason;
I have no idea about this. I'm just weighing into let you know that I'm still workng on your toroid winder. I've got the new computer now, with new software, so it's going to have to wait until I get used to it. (And I don't even want to burden you with the horror of trying to do graphics with a track-pad.)

 

[Jdo300]

Hi, Jason;
I have no idea about this. I'm just weighing into let you know that I'm still workng on your toroid winder. I've got the new computer now, with new software, so it's going to have to wait until I get used to it. (And I don't even want to burden you with the horror of trying to do graphics with a track-pad.)

Hi Danger,

Thanks again for your help. I'm definitely going to look into making this since most of the stuff I am playing around with involves toroids (custom ones).

 

[berkeman]

A few comments:

-- I'm not familiar with the concept of Lenz forces. There is Lenz's Law:

http://www.answers.com/topic/lenz-s-law

and the Lorentz force. I could be missing something, of course, but I'm not familiar with what you are asking about. Do you have a web pointer to an explanation of the Lenz force?

-- The toriod is not a system where you usually try to introduce external magnetic fields. You can, and there are definitely some subtleties about how susceptible the toroid is to external flat B fields, but you don't usually introduce them intentionally.

-- Is there some physical situation that you are trying to deal with for this question? The B field orientations and magnet movement are a bit off from any practical situation that I can picture.

-- Finally, keep in mind that introducing a permanent magnet that close to any transformer core will likely saturate the core, and spoil transformer action.


EDIT -- Oh, and in your drawing, the magneic poles are parallel to the toroid coils, not at 90 degrees to the coils.

 

[Jdo300]

Hi Berkeman,

Thanks for the correction about the coil direction. And as another correction, I meant to refer to Lenz's law. I'm trying to see how toroidal coils (not used as transformers) behave when used as a generator. I know that in normal generators, once a load is placed on the coils, the fields produced by the coils drag against the permanent magnets in the generator making the shaft harder to turn. From what I understand, I believe this is due to the effects of Lenz's Law. So I was wondering how Lenz's law would play a role here in a toroidal setup where the magnetic fields would be contained inside the core.

Thanks,
Jason O

 

[berkeman]

Toroids are a bit weird to deal with at first, but make more sense in the end as you picture the B-fields.

We are initially taught in school that the toroid contains all the field, so toroidal transformers are good for B-immune applications. But that's not fully true. Take a look at the 2-winding, sector-wound transformer in your picture. It is true that the B-field generated by either coil will for the most part be confined to the toroidal core. However, an external flat B field that comes in parallel to the axis of the windings will couple into the core as it passes by, and will generate an EMF in each of the two windings if the B-field is oriented in the axis of the windings. So if you place a slug coil at the side of the toroid, in parallel with the windings, then the slug's B-field will spew out the end of the slug nearest to the toroid, and be pulled into the toroid ferrite and split between the two windings, and flow out the far end of the toroid ferrite and bend back around to re-enter the botom end of the slug.

Sector-wound toroids are susceptible to external B-field interference. Quiz question -- how would your wind a 2-winding toroidal transformer to avoid this kind of B-field pickup?

 

[Jdo300]

Hi Berkeman,

To answer your quiz question, could you wind the coils in a bifilar fashion so tha the fields cancel out? Or, could you completely enclose the toroid in a ferrite or metal container to shield it from outside interference?

Ok, I think I have a good idea of why the coils placed by the core will induce current in the coils. Are there any nifty equations out there dealing with toroidal geometries to figure out how much an outside field would affect the coils?

My other question is how does Lenz's law play a role here? If I were trying to make a low-load generator using the toroid as the windings, would you see a reduced Lenz effect because of the enclosed magnetic fields in the core, or would you still see a lot of drag from the coils once a load is applied?

Thanks,
Jason O

 

[berkeman]

To answer your quiz question, could you wind the coils in a bifilar fashion so tha the fields cancel out? Or, could you completely enclose the toroid in a ferrite or metal container to shield it from outside interference?

Shielding works, but is usually not practical on all 6 sides. Bifilar is close, but the answer is to wind both windings full-circumferential (either as a bifilar pair, or one winding on top of the other). For each winding, you want half the winding to see the interfering flux going one way, and the other half of the winding sees the flux going the other way. That way, the net interfering voltage pickup is zero.

Ok, I think I have a good idea of why the coils placed by the core will induce current in the coils. Are there any nifty equations out there dealing with toroidal geometries to figure out how much an outside field would affect the coils?

You use Laplace's equation to calculate how much of the external field gets pulled into the core geometry. I wrote a discrete simulation once to calculate how much field concentration we were getting with a high-perm toroidal transformer. The concentration factor depends on the width-to-length ratio of the ferrite pickup material, and a few other things. For the particular geometry that I analyzed, I got about a 2:1 concentration of the external field (the extenal flat interfering field was pulled in and concentrated by the high-mu core material).

My other question is how does Lenz's law play a role here? If I were trying to make a low-load generator using the toroid as the windings, would you see a reduced Lenz effect because of the enclosed magnetic fields in the core, or would you still see a lot of drag from the coils once a load is applied?

I'm not sure I understand the question. A toroid will not make an efficient electromagnetic machine -- you want to be able to couple magnetic flux into different coils efficiently, and the external shape of the toroid does not lend itself to external coupling. You want to be able to move flat surfaces close together in order to reduce the reluctance of the gap, and to efficiently use the field lines.