Verify Magnetic Induction Homework: 50A Copper Wire 0.5*10-2m

[subhradeep mahata]

Homework Statement

A current of 50A flows through a copper wire of diameter 0.5 * 10^-2m. The magnetic induction on its surface will be:
A)4*10²T B)4*10^-2 C) 4*10^-3 D)none of these

Homework Equations

The Attempt at a Solution

I just want to verify my solution, as the answer keys are currently not available. I did the following things:

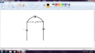
It shows the copper wire, and i have considered a cylindrical strip of infinitesimal radius at the base of the wire(shaded gray). Now, a current flows through it, magnitude 50A. We consider the upper surface, which is at a distance of 0.5*10^-2m. Since the strip of wire we have considered is very very close to all the points on the upper surface, we can compare it to an infinitely long current carrying wire, and we find the magnetic field due to this infinitely long wire at a point 0.5*10^-2m form it.
Accordingly,
magnetic field = μI/2πd
which come out to be 4*10^-3 after a hell lot of approximation.
Please tell me it it is correct or not, and suggest me some alternative solutions.

 

[Delta2]

I think you got the correct answer but with the wrong way. The main mistake in your approach is that the current is not flowing in that thin greyed strip but it is evenly distributed through the volume of the wire.

Because we have cylindrical symmetry in this problem , and also we are interested for the magnetic field on the surface (what it is following will not be correct if we are interested for the magnetic field in the interior of the wire) , you can assume that the current is flowing through a thin line that coincides with the central axis of the wire. Calculate then the magnetic field at distance $r=\frac{d}{2}$ from the center (that is where the surface of the wire is located) where $d$ is the diameter of the wire.

EDIT: BTW, the statement of the problem is a bit misleading. We are interested for the magnetic field intensity, not the magnetic induction.

 

[subhradeep mahata]

Yup, got it. I completely ignored the cylindrical symmetry.So, we are basically using this formula: μI/2πr
I also derived a general formula for finding the magnetic field at any arbitrary point P inside a conductor: μIr / 2πR^2 where r=distance of point P from the center of the circular cross section of the wire and R is the radius of the wire. (please verify it)

Yes, I know that it is quite misleading. For example, we are required to find the "magnetic induction" at point P:

(radius and lengths are given)
I was completely blank at this problem. Later, when I looked at the solution, it just showed we have to find the net magnetic field at point P. From then on, I developed the notion that magnetic field strength and magnetic induction are same!

 

[Delta2]

Yes your formula for the magnetic field strength in the interior of a cylindrical wire is correct.

There is no quantity labelled magnetic induction in physics, magnetic induction is instead the name of a physical phenomenon. The quantities involved are magnetic field strength (or magnetic field intensity) and magnetic field flux (through a given surface).

 

[subhradeep mahata]

Ok, thanks.

 

[rude man]

"Magnetic induction" is the accepted term for B.
In additionto B, which is tesla in mks, and flux, which is tesla*m^2, there is also H = B/μ = "magnetic field strength".
You will encounter this often, probably. For example, ampere's law is nicely expressed as H = I/2πR in your problem, avoiding the complexity of using μ which is Henry/m in mks.
Another example is the fundamental Maxwell equation ∇ x H = j + ∂D/∂t.
If you get into nonlinear magnetics, like transformer cores, you have to segregate H from B since μ is then a function of current whereas H is proportional to current.