Janji
- 5
- 0
Member warned that some effort must be shown
- Homework Statement
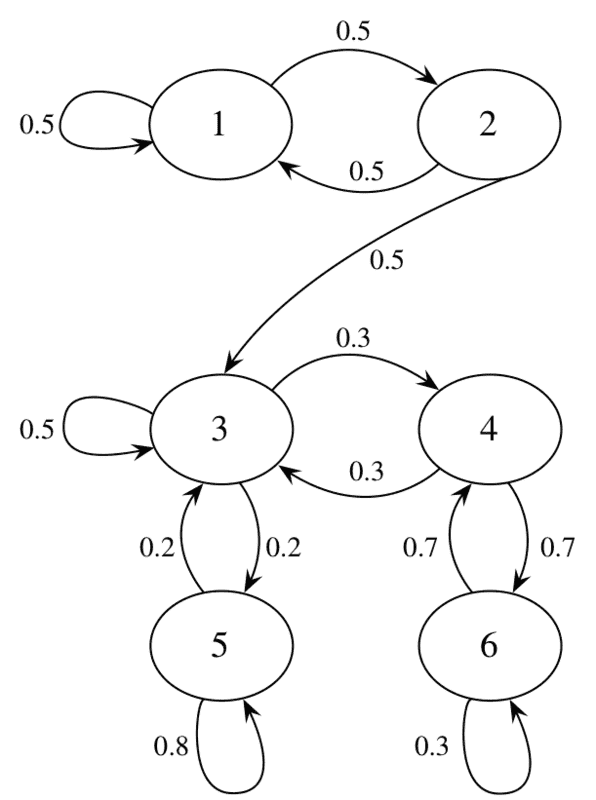
- Let's suppose the chain starts at state 1. The distribution of the number of times that the chain returns to state 1 is geometric and the parameter would be 1/4.
- Relevant Equations
- In the long run, what fraction of the time does the chain spend in state 3?
I need this for a programming project. Could you help?
Last edited by a moderator: